[알고리즘] 스트링 알고리즘

스트링 알고리즘

• 스트링(string) : 문자가 연속적으로 나열된 문자열 (ex. ATATCGCCCACGTAT)
• 알파벳(∑) : 스트링에 사용되는 문자들의 집합 (ex. ∑={A,C,G,T})
• 스트링 매칭, 스트링 압축 등의 문제를 해결하는 알고리즘

스트링 매칭

• 텍스트에서 패턴이 나타나는 위치를 찾는 것
• 텍스트의 길이 n은 패턴의 길이 m보다 크거나 같다.

브루트-포스 스트링 매칭알고리즘

• 텍스트의 각 위치에서부터 패턴의 길이만큼 문자를 비교하며 매치를 찾는 방법

const T = "AABAABAABAA";
const P = "AABAA";

const checkMatchIndex = (T, P) => {
  let result = [];
  for (let i = 0; i <= T.length - P.length; i++) {
    for (let j = 0; j < P.length; j++) {
      if (T[i + j] !== P[j]) break;
      if (j === P.length - 1) {
        result.push(i);
      }
    }
  }
  return result;
};

console.log(checkMatchIndex(T, P));
// [0, 3, 6]

시간복잡도

• O(nm)

라빈-카프 알고리즘

• 패턴의 해시값으로 매치의 후보를 찾고, 후보에 대해서만 문자별로 비교해서 매치를 찾는 방법
• 직전 위치의 해시값을 이용하여 상수 시간에 계산 가능

시간 복잡도

• O(n+km) (k: 매치의 개수)
  • 전처리 : O(m)
  • 텍스트에서 해시값 계산 : O(n)
  • 후보 위치는 문자 직접 비교, 매치 개수 k : O(km)
• 최선 : 매치 개수가 상수라면 O(n)
• 최악 : 모든 자리에서 매치가 발생하면 O(nm)이다.

KMP 알고리즘

• 패턴 내의 문자들의 관계를 이용하여 매칭 시 중복된 비교를 줄임
• 매치되는 위치를 찾은 후 패턴의 앞부분(접두부)과 뒷부분(접미부)이 최대로 일치하는 서브스트링의 접두부의 끝 문자 위치를 다음에 비교할 위치로 적용한다.

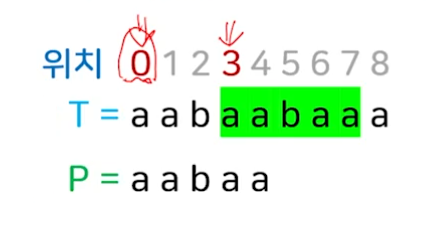
• 텍스트 T=’aabaabaaa’, 패턴 P=’aabaa’ 일 때, 위치 0에서 텍스트와 패턴의 문자를 비교하여 매치를 찾게 된다.
• 패턴의 접두부와 접미부가 최대로 일치하는 서브스트링이 ‘aa’이므로 위치 4에 접두부의 끝 문자의 위치인 1이 위치하도록 적용하여 위치 5부터 ‘baa’를 비교하면 된다. (f₄=1)
• 접두부와 접미부의 최대 일치가 없으면 -1이다. 이 때는 패턴을 적용한 위치를 건너뛰고 다음 위치부터 비교한다.

// 접두부와 접미부의 최대 일치 서브스트링을 찾는 전처리 알고리즘
function preKMP(pattern) {
  const lps = new Array(pattern.length).fill(0);
  let length = 0;
  let i = 1;

  while (i < pattern.length) {
    if (pattern[i] === pattern[length]) {
      length++;
      lps[i] = length;
      i++;
    } else {
      if (length !== 0) {
        length = lps[length - 1];
      } else {
        lps[i] = 0;
        i++;
      }
    }
  }

  return lps;
}

// KMP 알고리즘
function KMPSearch(text, pattern) {
  const lps = preKMP(pattern);
  const result = [];
  let i = 0; // text의 인덱스
  let j = 0; // pattern의 인덱스

  while (i < text.length) {
    if (pattern[j] === text[i]) {
      i++;
      j++;
    }

    if (j === pattern.length) {
      result.push(i - j);
      j = lps[j - 1];
    } else if (i < text.length && pattern[j] !== text[i]) {
      if (j !== 0) {
        j = lps[j - 1];
      } else {
        i++;
      }
    }
  }

  return result;
}

// 예제 사용
const text = "aacaabaabaa";
const pattern = "aabaa";
const result = KMPSearch(text, pattern);

시간복잡도

• 전처리 : O(m)
• 매칭 : O(n)
• n≥m 이므로 전체 성능은 O(n)

보이어-무어 알고리즘

• 패턴 내의 문자들의 관계를 이용하여 매칭 시 중복된 비교를 줄임
• 텍스트의 첫 위치에서 패턴의 뒷부분부터 문자 비교
• 불일치 또는 매치를 발견하면 불일치 문자 방법과 일치 접미부 방법 중 더 많이 이동시킬 수 있는 값 선택
  • 불일치 문자 방법 : 불일치한 텍스트의 문자가 패턴에서 가장 마지막에 나타나는 위치로 패턴을 이동
  • 일치 접미부 방법 : 일치한 서브스트링의 접미부에 대해 접두부와 접미부의 최대 일치 정보만큼 패턴을 이동
    • KMP 알고리즘은 문자의 왼쪽에서 오른쪽으로 비교하고 패턴의 왼쪽 서브스트링에 대해 전처리하지만, 보이어-무어 알고리즘은 문자의 오른쪽에서 왼쪽으로 비교하고 패턴의 오른쪽 서브스트링에 대해 전처리한다.

시간복잡도

• 전처리 : O(m)
• 최선 : O(n/m)
• 최악 : O(nm)

스트링 압축

RLE

• 스트링에서 연속으로 나타나는 문자와 반복 횟수로 압축하는 방법
• 인코딩 예 → aaaaabb → (a,5) (b,2)
• 디코딩 예 → (a,5) (b,2) → aaaaabb

성능

• O(n)