[알고리즘] 탐색2 - 해시 테이블

해시 테이블

• 각 위치(슬롯)마다 주소가 부여되어 있는 저장공간으로 기본적으로 배열의 형태로 볼 수 있다.
• 해싱 : 탐색 키 값을 활용하여 해시 테이블의 주소를 계산하는 방법

해시 함수

• 키 값을 테이블의 주소로 변환하는 함수
• 서로 다른 키 값이 해시 테이블의 같은 주소로 변환되는 충돌이 적게 발생되도록 해야 한다.

정수를 위한 해시 함수

입력 데이터가 정수인 경우에 적합

• 제산 잔여법
  • h(K) = K mod M (K: 키 값, M: 해시 테이블의 크기)
  • M의 값은 2의 거듭제곱과 상당한 차이가 있는 소수로 선택하는 것이 바람직하다.
• 비닝
  • 키의 집합 U를 M등분하여 각 등분을 각 슬롯으로 해시하는 방법
  • 만약 키 값의 범위가 0~999까지의 정수이고 해시 테이블의 크기가 10이면 키 값을 1000/10=100 개씩 나눠서 각 슬롯에 해시한다.
• 중간 제곱법
  • 주어진 키값을 제곱하여 제곱한 결과에서 하위 m을 버리고, M에 해당하는 하위 r비트를 취한다.

문자열을 위한 해시 함수

입력 데이터가 문자열인 경우에 적합

• 비닝
  • 키의 집합 U를 M등분하여 각 등분을 각 슬롯으로 해시하는 방법
  • 문자열의 앞쪽 일부를 해시 결과로 사용한다.
  • 문자열의 앞쪽의 분포가 고르지 못하면 결과가 슬롯에 고르게 분포되지 못함
• 단순 합
  • 각 문자의 코드값을 합한 후 제산 잔여법 적용
  • 짧은 문자열에는 비효과적
  • 문자의 출현 순서는 고려되지 않음(h(‘ABC’) = h(‘BCA’))
• 가중 합
  • 각 문자의 코드값에 자리에 따른 가중치를 곱한 값을 합한 후 제산 잔여법을 적용
  • 문자의 출현 순서를 고려한다. (h(‘ABC’) != h(‘BCA’))

충돌 해결 방법

충돌 : 서로 다른 키 값 x,y에 대하여 h(x)=h(y)인 경우

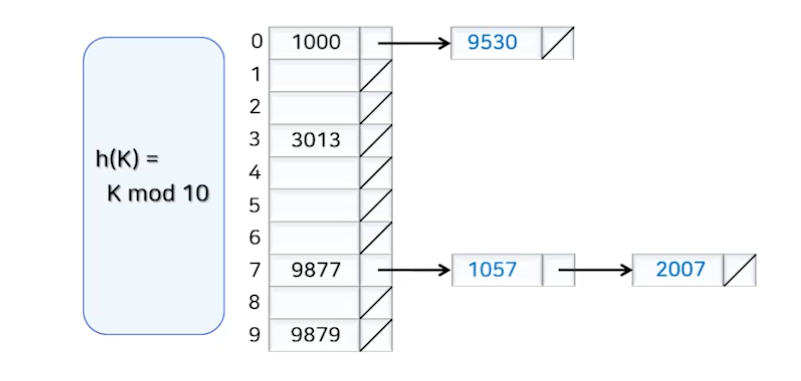
개방 해싱 (연쇄법)

• 충돌된 데이터를 테이블 밖의 별도 장소에 저장/관리, 연결 리스트 사용
• 해싱 테이블의 각 슬롯을 연결 리스트의 헤더로 사용
• 해시 테이블과 연결 리스트가 주기억장치 내에서 유지될 때 적합

폐쇄 해싱 (개방 주소법)

• 해시 테이블의 다른 슬롯에 충돌된 데이터를 저장/관리
• 종류 : 버킷 해싱, 선형 탐사, 이차 탐사, 이중 해싱
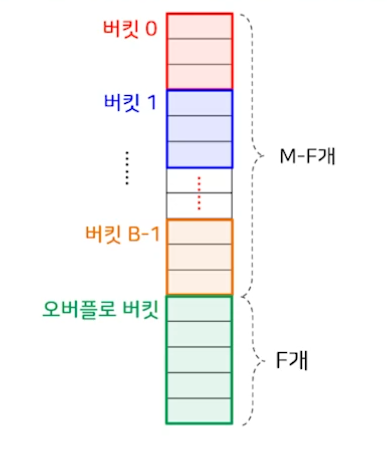
• 버킷 해싱 : 해시 테이블 슬롯을 버킷으로 묶어 버킷 단위로 해싱하고 버킷이 꽉 찼다면 데이터는 해시 테이블 끝의 오버플로 버킷에 저장된다.
• 선형 탐사 : 홈 위치가 사용 중이라면 빈 슬롯을 찾을 때까지 해시 테이블의 바로 다음 슬롯으로 순차적으로 이동. 만약 해시 테이블의 끝에 도달하면 다음 탐사 순서는 해시 테이블의 시작 위치이다.
  • 모든 슬롯이 새로운 데이터가 삽입될 후보가 됨
  • 1차 클러스터링이 발생하는 문제가 있다.
• 이차 탐사 : 탐사 순서의 계산에 이차식을 이용
  • 충돌이 발생하는 횟수의 제곱 형태로 탐사 순서를 결정
  • 서로 다른 홈 위치를 갖는 두 키는 서로 다른 탐사 순서를 가짐
  • 모든 슬롯이 탐사 순서에 사용되지 않음
  • 2차 클러스터링이 발생하는 문제가 있다.
• 이중 해싱 : 탐사 순서를 원래의 키값을 이용하여 해싱
  • 1차,2차 클러스터링 문제해결
  • 서로 다른 두 키의 홈 위치가 동일해도 서로 다른 탐사 순서를 가짐
  • 좋은 이중 해싱을 구하려면 탐사 순서에 있는 모든 상수가 해시 테이블의 크기 M과 서로 소가 되어야 함

삭제 연산

• 데이터의 삭제가 차후의 탐색을 방해하지 않아야 한다.
• 삭제로 생긴 빈 슬롯은 나중에 삽입 과정에서 사용되어야 한다.

비석

• 삭제된 데이터의 위치에 ‘비석’이라는 특별한 표시를 하는 방법
  • 탐색 : 탐색하는 동안 비석을 만나면 탐색을 계속 진행
  • 삽입 : 비석이 표시된 위치를 빈 위치로 간주하여 새 데이터 삽입
• 비석의 개수가 증가할수록 평균 탐색 거리가 증가한다.