[인공지능] 탐색에 의한 문제풀이

문제풀이

• 문제를 파악하고 문제의 해에 이르는 방법을 찾아내는 일련의 과정
• 상태묘사 : 풀이하고자 하는 문제의 상태를 컴퓨터로 처리하기 위한 적절한 자료구조로 표현한 것
• 연산자 : 어느 한 상태로부터 다른 상태로 변환하게 하는 역할
• 상태공간 : 정의된 연산자 집합을 이용하여 초기상태로부터 얻을 수 있는 모든 상태의 집합

상태 공간에서의 문제풀이

• 초기상태에서 시작하여 목표상태에 도달할 수 있는 일련의 연산자를 찾는 것

탐색 과정

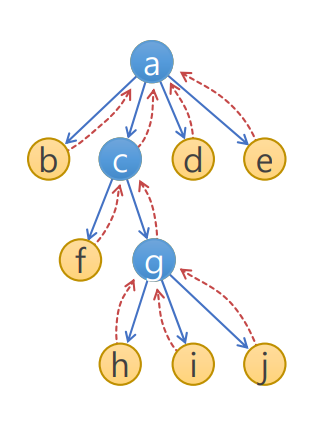
• 정해진 기준에 따라 노드를 선택하고, 선택된 노드(상태)에 적용할 수 있는 모든 연산자를 가하여 후계노드(후계상태)를 생성
• 후계노드에 부모노드를 가리키는 포인터를 첨부하여 경로를 알 수 있도록 함
• 원하는 목표를 찾지 못하면 다음 노드를 선택하여 탐색 과정을 반복
• OPEN : 앞으로 확장할 노드를 저장하는 리스트 (ex. {(b,a), (d,a), (e,a), (f,c), (h,g), (i,g), (j,g)})
• CLOSED : 이미 확장한 노드를 저장하는 리스트 (ex. {(a,NULL), (c,a), (g,c)})

탐색 방법의 종류

타입	임의 경로 탐색	최적 경로 탐색
맹목적 탐색	깊이우선 탐색, 너비우선 탐색	균일비용 탐색
경험적 탐색	언덕오르기 탐색, 최적우선 탐색, 모의 담금질	A* 알고리즘

맹목적 탐색

• 목표노드의 위치와 무관한 순서로 노드 확장
• 매우 소모적인 탐색을 할 가능성이 높음

깊이우선 탐색

• 탐색 깊이 방향으로 계속 전진하여 목표를 탐색하는 방법
• 가장 최근에 생성된 노드를 가장 먼저 확장하는 스택 구조이다.
• 목표에 도달할 수 없는 경로를 계속 탐색할 수 있으므로 이를 해결하기 위해 깊이제한을 정할 수 있다.
• 더 이상 진행할 경로가 없으면 이전 상태 중 다른 경로를 선택할 수 있는 위치로 복귀하여 탐색을 계속한다.

너비우선 탐색

• 트리의 레벨 순서에 따라 노드를 확장한다.
• 생성된 순서에 따라 노드를 확장하는 큐 구조이다.
• 해가 존재한다면 출발노드에서 목표노드까지 도달하는 최단길이 경로를 찾는 것을 보장한다. (최초로 찾게 되는 해가 최단길이를 갖는 해가 된다.)

균일비용 탐색

• 출발노드로부터의 경로비용이 최소인 노드를 선택하여 확장
• 최소비용 경로를 탐색할 수 있다.

예제

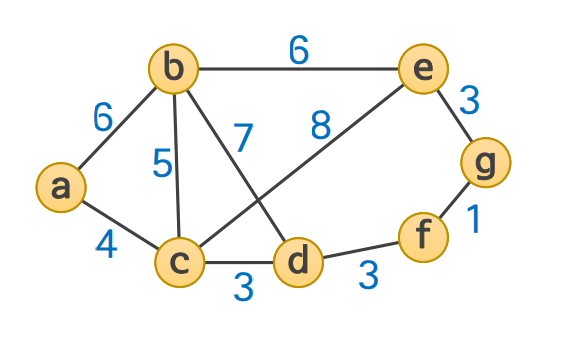
a, b, c, d, e, f, g라는 7개의 도시를 연결하는 도로망이 건설되어 있다. 어떤 여행자가 도시a를 출발하여 도시g까지 가는 경로를 찾고자 한다. 다음 그림은 각 도시를 연결하는 도로와 그 거리를 그래프로 표현한 것이다. 균일비용 탐색을 하여 최단길이 경로를 탐색하라.

• OPEN에서 노드 a를 꺼내어 확장하고 이를 CLOSED에 넣는다. 확장결과 노드 b와 노드 c가 생성된다. 이들을 OPEN에 넣는다.
• 노드 b와 노드c의 경로비용을 비교하여 노드 c가 더 작으므로 노드 c를 꺼내어 확장하고 이를 CLOSED에 넣는다. 확장 결과 노드 b,d,e가 생성된다. 노드 b는 이미 OPEN에 있으므로 노드 d,e만 OPEN에 넣는다.
• 이와 같은 과정을 반복하여 탐색 결과 최단길이 경로는 a→c→d→f→g이며, 거리는 11이다.

경험적 탐색

• 목표노드의 위치와 관련된 경험적 정보를 사용
• 경험적 정보 : 항상 옳은 것은 아니지만, 개연성이 있어 많은 경우 잘 맞는 정보
• 경험적 정보를 평가함수에 반영
• 평가함수 : 어떤 상태가 주어졌을 때 그 상태를 거쳐가는 것이 목표상태로 가는데 얼마나 바람직한가를 나타내는 함수

언덕오르기 탐색

• 후계노드의 평가함수를 계산하여 비용이 가장 적은 노드를 확장
• 후계노드까지 도달하는데 사용된 비용은 고려하지 않음
• 등산 문제 (산의 정상에 도달하는 방법)
  • 상태 : 등산가의 좌표 및 고도
  • 연산자 : 동, 서, 남, 북 방향으로 정해진 거리만큼 이동
  • 목표상태 : 모든 후계상태의 고도가 현재상태보다 낮은 상태
  • 확인된 위치 중 가장 높은 곳으로 이동한다. (최급상승법)

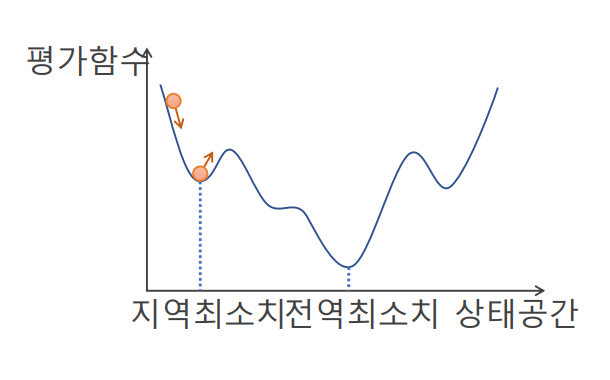
언덕오르기 탐색의 문제점

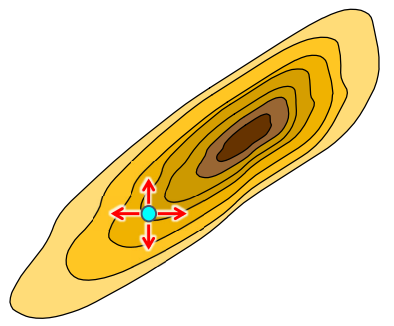
• 지역최대치 문제 : 정상 외에 여러 봉우리가 있을 때, 그 봉우리에 올라가면 현재상태를 개선하지 못한다.
• 고원문제 : 현재 고도가 평평한 곳에 있는 경우 어느 방향으로 가더라도 현재상태를 개선하지 못한다.
• 능선문제 : 대각선의 고도는 높지만 동서남북의 후계노드의 고도가 낮은 경우 현재상태를 개선하지 못한다.

모의 담금질

• 평가함수의 전역최소치 또는 전역최대치에 해당되는 해를 구하기 위한 확률적 접근방법
• 후계노드 중 평가함수가 최대인 노드를 선택하는 대신 임의의 후계노드를 선택한다.
• 만일 선택한 후계노드가 개선된 상태를 나타낸다면 그 후계노드를 차기상태로 선택하고, 개선하지 못한다면 그 후계노드를 선택할 확률을 1보다 작은 값이 되도록 한다.
• 현재상태로 평가함숫값이 더 큰 상태로 이동할 확률은 시간에 따라 감소한다.
• 시간이 많이 소요된다.

A* 알고리즘

• 평가함수 f’(n) = g(n) + h’(n)
  • g(n) = 출발노드로부터 현재노드 n까지의 경로비용
  • h’(n) = 현재노드 n부터 목표노드까지의 예측 경로비용
• 후계노드중에서 f’(n)이 최소인 노드를 선택하여 확장한다.
• 노드가 중복 생성된 경우
  • 동일한 노드가 OPEN에 존재하는 경우 : 평가함숫값이 더 큰 노드를 제거
  • 동일한 노드가 CLOSED에 존재하는 경우 : 나중에 생성된 노드를 제거
• 만일 어떤 노드로부터 목표노드까지 도달하는 경로비용을 예측한 값이 항상 실제 비용 이하라면(h’(n)≤h(n)) 최소비용 경로를 탐색하는 것을 보장한다.

예제

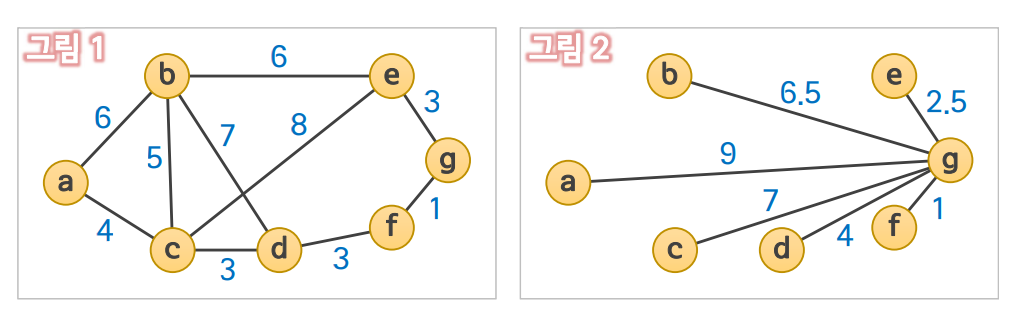
a, b, c, d, e, f, g라는 7개의 도시를 연결하는 도로망이 건설되어 있다. 어떤 여행자가 도시a를 출발하여 도시g까지 가는 경로를 찾고자 한다. 그림1은 각 도시를 연결하는 도로와 그 거리를 표현한 그래프이고, 그림2는 각 도시로부터 목적지인 g까지의 직선거리이다. A* 알고리즘을 이용하여 최단길이 경로를 탐색하라.

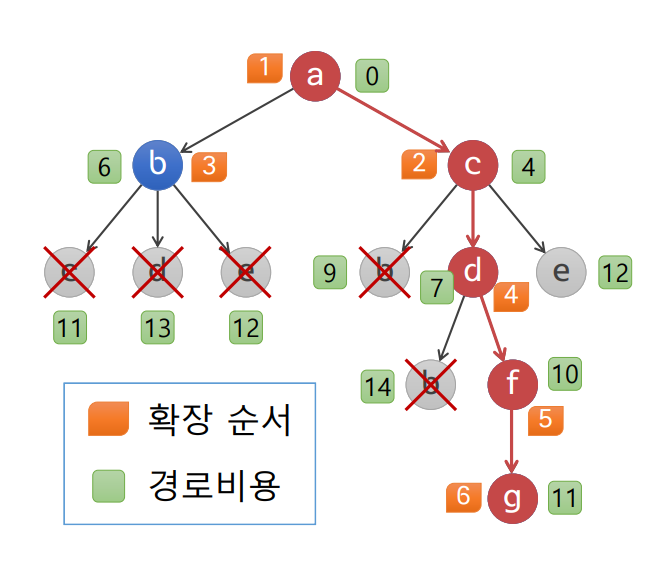
1. 시작 노드인 a가 맨 처음 확장된다. 확장결과 노드 b와 노드 c가 생성된다. 이들을 OPEN에 넣는다.
2. OPEN에 존재하는 노드 중 c의 평가함숫값이 가장 작으므로 두 번째로 확장된다. 확장결과 노드 b,d,e가 생성된다. 노드 b는 이미 OPEN에 존재하는 노드 b보다 평가함숫값이 크므로 삭제된다.
3. OPEN에 존재하는 노드 중 d의 평가함숫값이 가장 작으므로 d가 세 번째로 확장된다. 확장결과 노드 b,f가 생성된다. 노드 b는 이미 OPEN에 존재하는 노드 b보다 평가함숫값이 크므로 삭제된다.
4. OPEN에 존재하는 노드 중 f의 평가함숫값이 가장 작으므로 f가 네 번째로 확장된다. 확장결과 노드 g가 생성된다.
5. OPEN에 존재하는 노드 중 g의 평균함숫값이 가장 작으므로 g가 선택된다. g는 목표노드이므로 탐색이 종료된다. 탐색결과 최단 경로는 a→c→d→f→g이며, 거리는 11이다.

각 노드에서 목적지인 노드 g까지의 직선거리는 각 노드에서 g까지의 실제 비용보다 항상 작거나 같으므로 h’(n)≤h(n)이 성립하여 최소비용 경로를 탐색하는 것을 보장한다.