[데이터베이스 시스템] 정규화

나쁜 릴레이션

• 데이터의 중복
• 갱신 이상
  • 삽입 이상 : 레코드 추가 시 불필요한 컬럼의 값 없이는 추가하지 못하는 경우
  • 삭제 이상 : 삭제 시 의도하지 않았던 다른 데이터가 삭제되는 경우
  • 수정 이상 : 중복 저장된 레코드를 수정 시 모두반영이 안되어 일관성이 깨지는 경우

함수적 종속성

• 릴레이션 인스턴스를 분석하여 속성들 간의 연관관계를 표현한 것
• 릴레이션의 효율성을 향상시켜 좋은 릴레이션으로 변환하는데 이용
• 임의의 릴레이션 스키마 R의 인스턴스에 포함되는 서로 다른 두 레코드 r₁, r₂와 속성(컬럼) 집합 X와 Y에 대해, r₁[X]=r₂[X]일 때, r₁[Y]=r₂[Y]이면 함수적 종속성 X→Y가 성립한다.

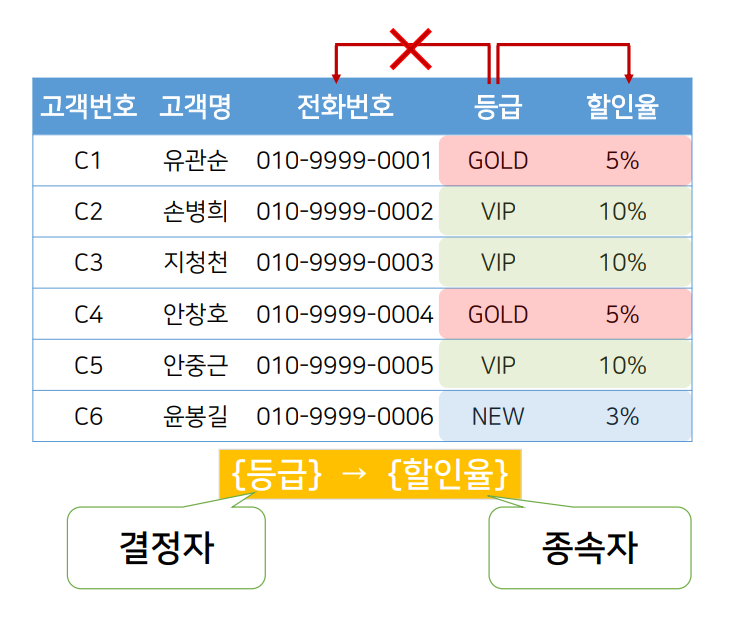
위 릴레이션에서 등급과 할인율에 대한 연관성을 함수적 종속성이라고 하며 {등급}→{할인율}로 표기한다. (등급=결정자, 할인율=종속자)

함수적 종속성의 추론

암스트롱 공리

• 재귀성 규칙 : 𝑋⊇𝑌이면, 𝑋→𝑌이다.
• 부가성 규칙: 𝑋→𝑌이면, 𝑋𝑍→𝑌𝑍이다.
• 이행성 규칙: 𝑋→𝑌이고, 𝑌→𝑍이면, 𝑋→𝑍이다.
• 분해 규칙: 𝑋→𝑌𝑍이면, 𝑋→𝑌이다.
• 합집합 규칙: 𝑋→𝑌이고, 𝑋→𝑍이면, 𝑋→𝑌𝑍이다.
• 의사 이행성 규칙 : 𝑋→𝑌이고, 𝑊𝑌→𝑍이면, 𝑊𝑋→𝑍이다

카노니컬 커버

• 함수적 종속성 추론 규칙으로 확장된 클로저에는 자명한 종속성과 중복된 종속성을 포함
• 불필요한 함수적 종속성을 제거한 표준형으로 변환 후 정규화를 수행
• 표준형 조건
  • F의 모든 함수적 종속성의 오른편 속성(종속자)은 반드시 1개이다.
  • F에서 X→A를 X의 진부분집합 Y에 대하여 Y→A로 교체했을 때, 그 집합이 F와 동등한 집합이 불가능
  • F에서 어떤 함수적 종속성을 제거했을 때, 그 집합이 F와 동등한 집합이 불가능

정규화의 기능

• 어떠한 릴레이션이라도 데이터베이스 내에서 표현할 수 있도록 만든다.
• 보다 간단한 관계 연산에 기초하여 검색 알고리즘을 효과적으로 만든다.
• 바람직하지 않은 삽입, 갱신, 삭제 이상(anomaly) 현상을 제거한다.
• 새로운 형태의 데이터가 삽입될 때 릴레이션 재구성의 필요성을 줄인다.

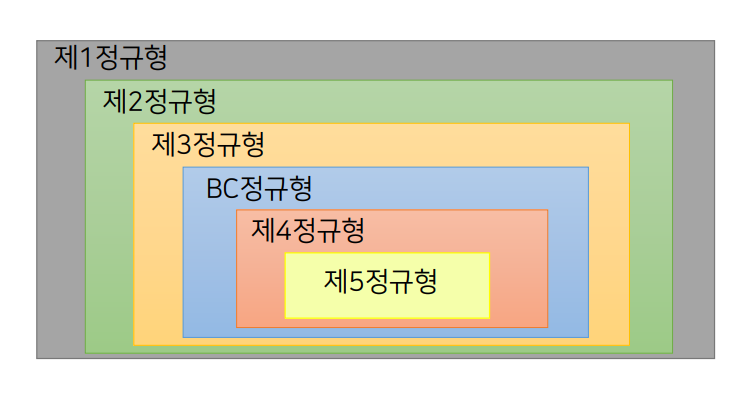
정규화 과정

• 제1 정규형에서 제5 정규형으로 갈수록 조건이 까다로움

제1 정규형

• 관계형 모델의 조건에 따라 자동 적용되는 정규형
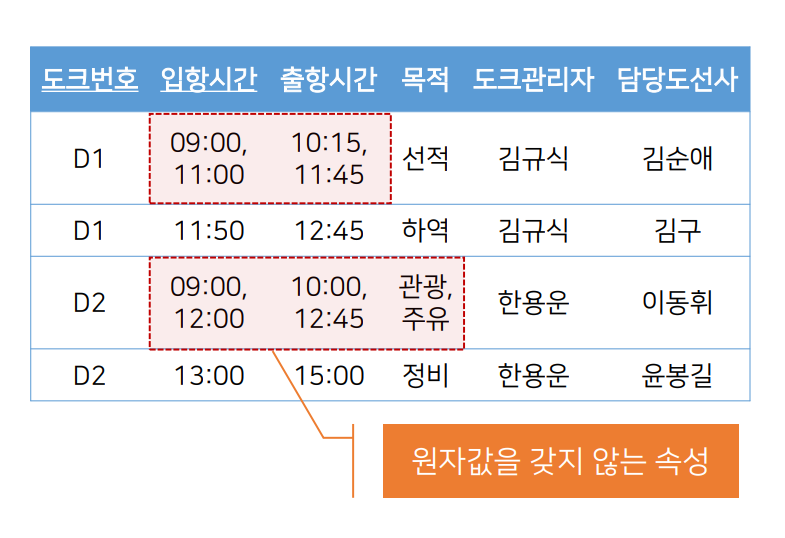
• 릴레이션 스키마에서 정의된 모든 속성의 도메인이 원자값을 갖는 상태여야 한다.

제2 정규형

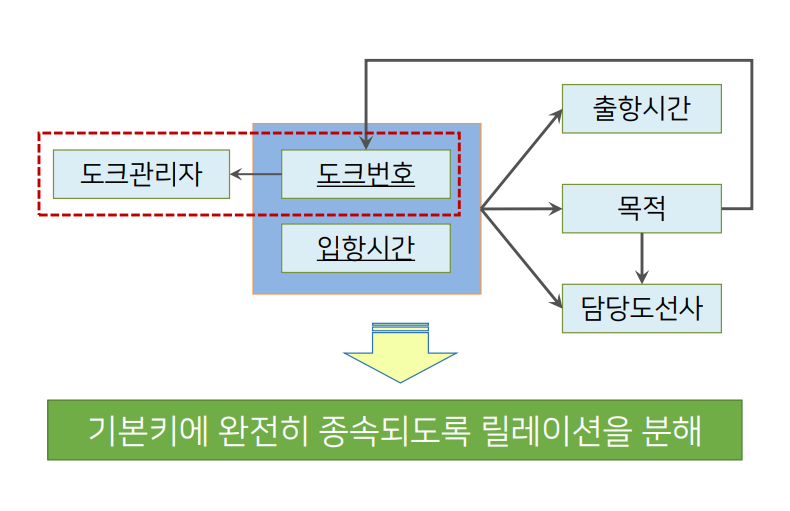
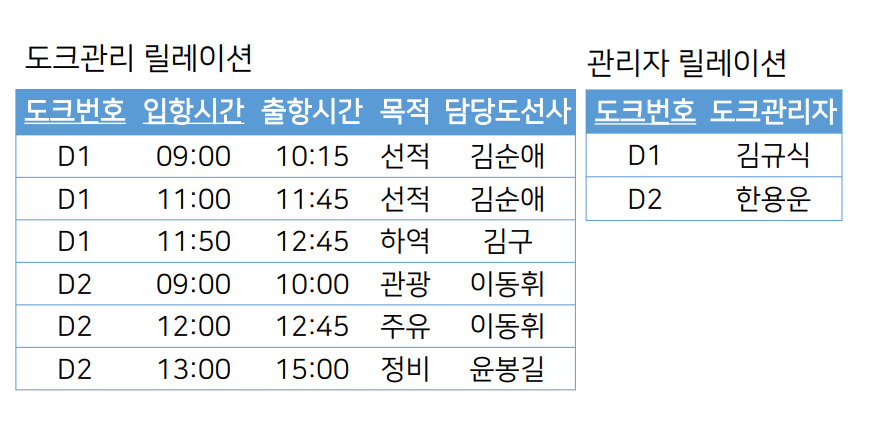
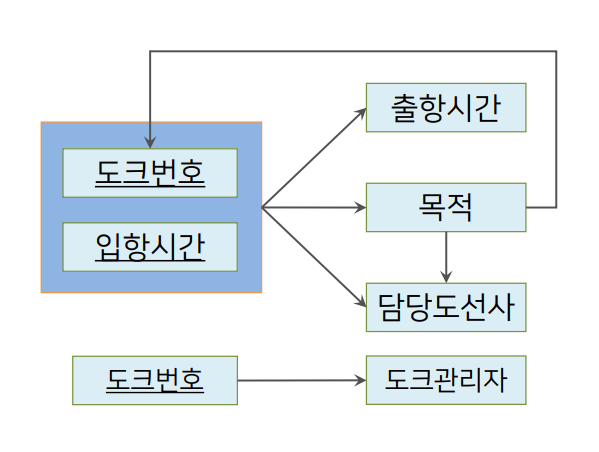
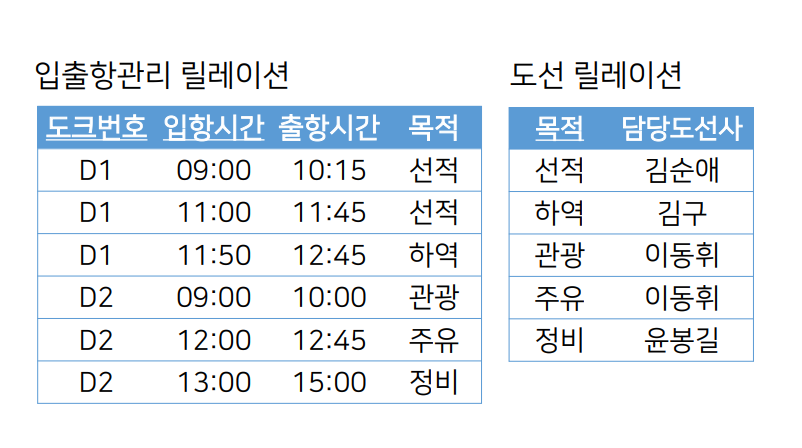
• 기본키가 아닌 속성들이 기본키에 완전히 종속되어 있는 상태여야 한다.
• 위 종속성 다이어그램에서 도크관리자는 도크번호에 부분 함수 종속되어 있다. (기본키 ‘도크번호+입항시간’에 완전 종속 되어야 함)
• 기본키가 완전히 종속되도록 릴레이션을 분해한다.
• 무손실 분해 : 스키마 𝑅에 함수적 종속성 X→Y가 존재하고 X∩Y=∅이면, 𝑅을 𝑅−𝑌와 XY로 분해
  • 도크번호와 도크관리자가 같은 컬럼을 공유하고 있지 않다면 도크관리자 컬럼을 떼어내 분리한다.

제3 정규형

• 기본키가 아닌 속성들이 어떤 키에도 이행적으로 종속되지 않은 상태여야 한다.
• 이행적 종속성 : X→Y이고 Y→Z이면 X→Z이다.
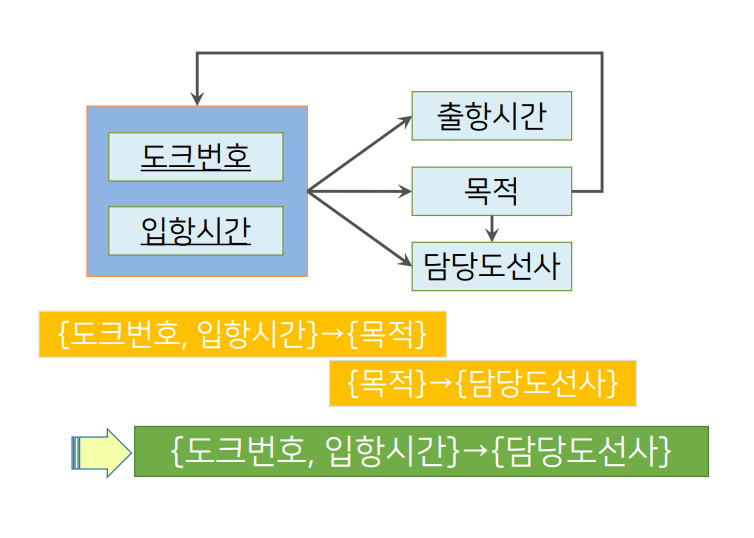
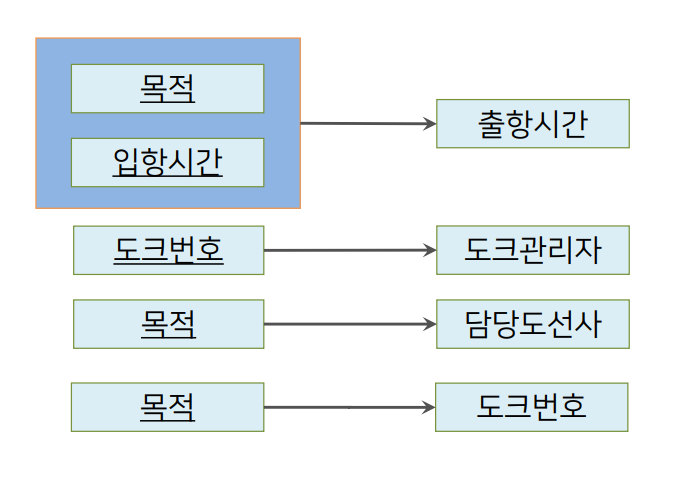
• 위 종속성 다이어그램에서 {도크번호, 입항시간}→{목적}, {목적}→{담당도선사}이므로 {도크번호, 입항시간}→{담당도선사}이 되어 이행적으로 종속된다.

BC정규형

• X→Y 형태의 모든 함수적 종속성에 대하여 X가 수퍼키인 상태여야 한다.
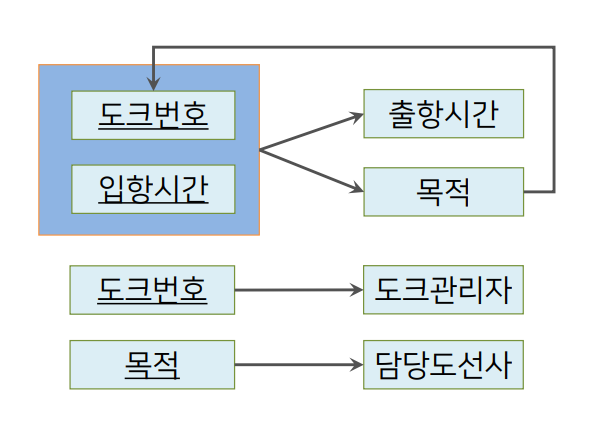
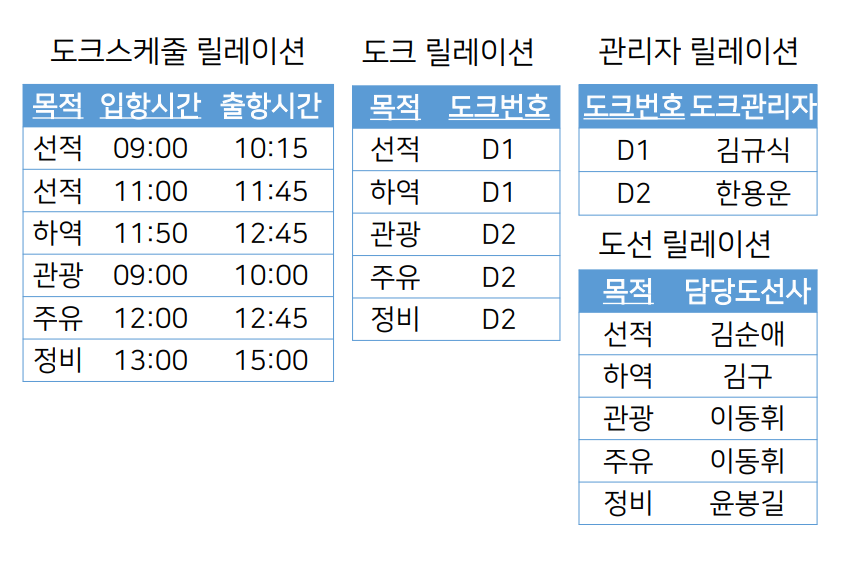
• 위 종속성 다이어그램에서 {목적}→{도크번호}이고, 목적이 수퍼키가 아니므로 릴레이션을 수정한다.
• 이 때 목적이 도크번호의 결정자이므로 기본키에서 도크번호를 목적으로 대체하고, 도크번호를 떼어내 분리한다.

역정규화

• 정규화의 반대 과정
• 조인연산으로 정규화로 분할한 릴레이션을 모두 조인함