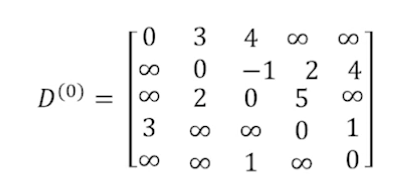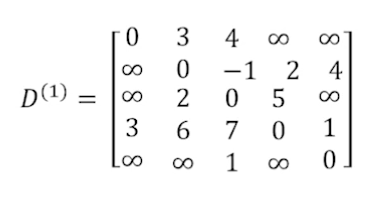[알고리즘] 그래프2

최단 경로

• 두 정점 u와 v간의 최단 경로 : 가중 그래프에서 두 정점 u에서 v를 연결하는 경로 중 간선의 가중치의 합이 가장 작은 경로
• 최단 경로 문제의 유형
  • 단일 출발점 최단 경로 문제 : 데이크스트라 알고리즘, 벨만-포드 알고리즘
  • 모든 쌍 최단 경로 문제 : 플로이드 알고리즘

단일 출발점 최단 경로

데이크스트라 알고리즘

• 욕심쟁이 방법
• 출발점에서 시작하여 거리 d[]가 최소인 정점을 차례대로 선택하여 최단 경로를 구하는 방법
• 음의 가중치를 갖는 간선이 없어야 한다.
• 초기화 : 출발점 s의 거리 d[s]=0, 나머지 모든 정점 v의 거리 d[v]=∞, 선택된 정점의 집합 S={}
• S=V가 될 떄까지 반복
  • 미선택 정점 집합 V-S에서 거리 d[]가 가장 작은 정점 u를 선택
  • u의 인접 정점에 대해서 u를 경유하는 거리와 기존 거리를 비교해서 작은 값을 새로운 거리값으로 조정

예제

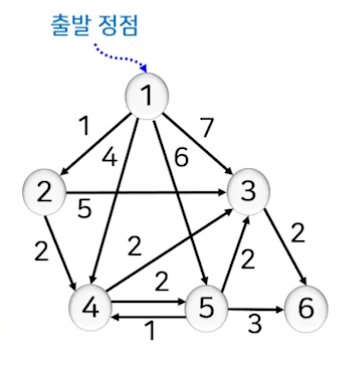
주어진 그래프에 대해서 데이크스트라 알고리즘을 적용하여 최단 경로를 구하시오. 단, 출발점은 1이다.

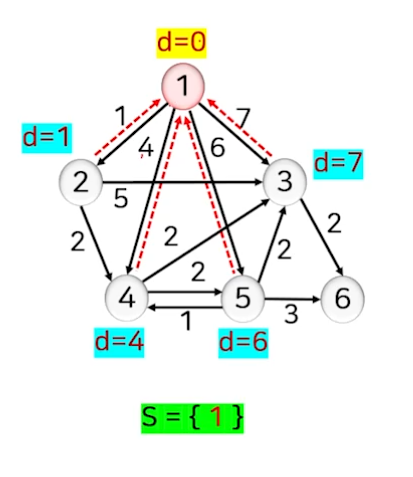
• 정점 1을 선택된 정점 집합 S에 추가한다.
• 정점 1에 인접한 정점(2,3,4,5)의 거리는 기존 거리 d[]=∞보다 정점 1을 경유하는 거리가 작으므로 ‘정점 1까지의 거리 d[1]+해당 간선의 가중치’를 새로운 거리값으로 조정한다.
• 거리가 조정된 인접 정점의 선행 정점을 prev[v]=1로 지정한다.

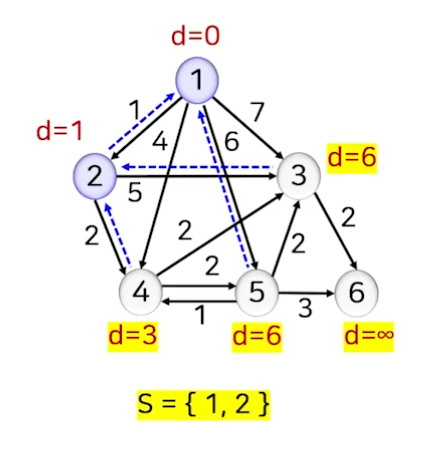
• 미선택 정점 집합 중 거리 d[]가 가장 작은 정점 2를 선택하고 S에 추가한다.
• 정점 2에 인접한 정점(3,4)의 거리는 기존 거리값보다 정점 2를 경유하는 거리가 작으므로 ‘정점 2까지의 거리 d[2]+해당 간선의 가중치’를 새로운 거리값으로 조정한다.
• 거리가 조정된 인접 정점의 선행 정점을 prev[v]=2로 지정한다.

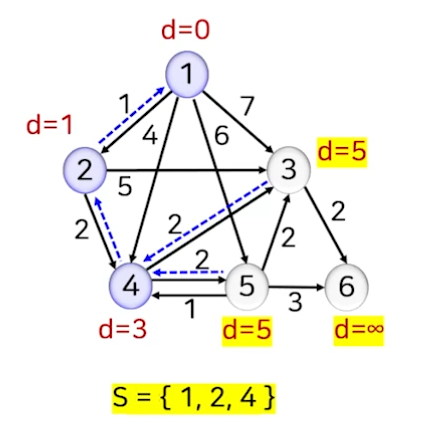
• 미선택 정점 집합 중 거리 d[]가 가장 작은 정점 4를 선택하고 S에 추가한다.
• 정점 4에 인접한 정점(3,5)의 거리는 기존 거리값보다 정점 4를 경유하는 거리가 작으므로 ‘정점 4까지의 거리 d[4]+해당 간선의 가중치’를 새로운 거리값으로 조정한다.
• 거리가 조정된 인접 정점의 선행 정점을 prev[v]=4로 지정한다.

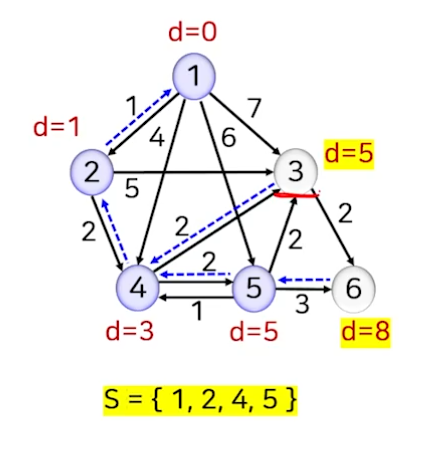
• 미선택 정점 집합 중 거리 d[]가 가장 작은 정점 5를 선택하고 S에 추가한다. (정점 3과 동일한 값이라 정점 3을 선택해도 무방하다.)
• 정점 5에 인접한 정점 6의 거리는 기존 거리값보다 정점 5를 경유하는 거리가 작으므로 ‘정점 5까지의 거리 d[5]+해당 간선의 가중치’를 새로운 거리값으로 조정한다.
• 거리가 조정된 인접 정점의 선행 정점을 prev[v]=5로 지정한다.

• 미선택 정점 집합 중 거리 d[]가 가장 작은 정점 3를 선택하고 S에 추가한다.
• 정점 3에 인접한 정점 6의 거리는 기존 거리값보다 정점 3를 경유하는 거리가 작으므로 ‘정점 3까지의 거리 d[3]+해당 간선의 가중치’를 새로운 거리값으로 조정한다.
• 거리가 조정된 인접 정점의 선행 정점을 prev[v]=3로 지정한다.

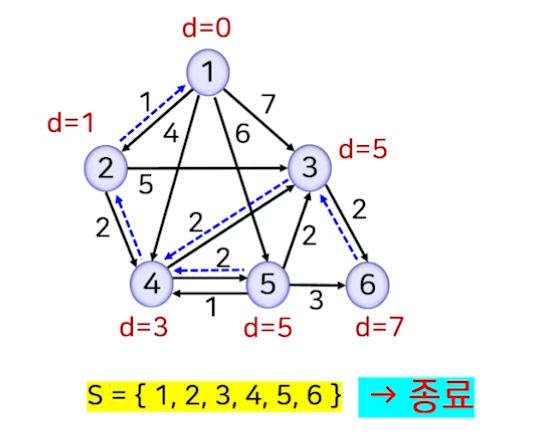
• 미선택 정점 집합 중 거리 d[]가 가장 작은 정점 6를 선택하고 S에 추가한다.
• 더 이상 남은 정점이 없으므로 종료한다.
• 최단 경로는 선행 정점을 나타내는 점선을 따라가면 된다.

성능

• 인접 행렬로 표현하면 O(|V|²), 인접 리스트로 표현하면 O((|V|+|E|)log|V|)

벨만-포드 알고리즘

• 음의 가중치를 갖는 간선이 존재하는 경우에도 처리 가능
• 간선을 1개부터 최대 n-1개까지 사용하는 최단 경로를 단계적으로 구해 나가는 방법
• 초기화 : 출발점 s의 거리 d[s]=0, 나머지 모든 정점 v의 거리 d[v]=∞
• 모든 간선을 한 번씩 조사하면서 기존 거리와 해당 간선을 지남으로써 결정되는 거리 중에서 작은값을 새로운 거리값으로 조정한다.
  • 이 과정을 n-1번 반복한다.
  • 모든 간선을 한 번씩 조사할 필요 없이 전 단계에서 거리값 d[]의 조정이 발생한 정점에 부수된 간선만 조사해도 된다.

예제

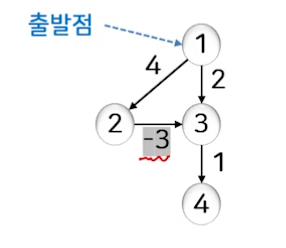
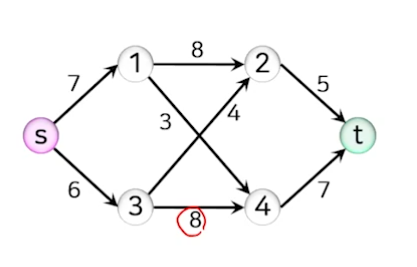
주어진 그래프에 대해서 단일 출발점 최단 경로를 구하시오. 단, 출발 정점은 1이다.

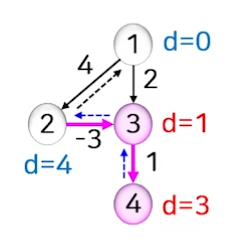
• 간선 1개를 사용한 최단 경로
  • 정점 1에 인접한 정점 2, 정점 3의 거리가 조정된다.

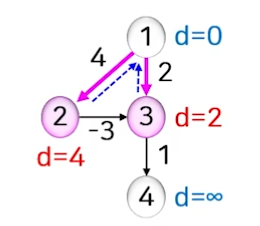
• 간선 2개를 사용한 최단 경로
  • 간선 <2,3>을 적용하면 d[3]이 2에서 1로 줄어들고, 간선 <3,4>로 인해 d[4]가 3으로 변경된다.

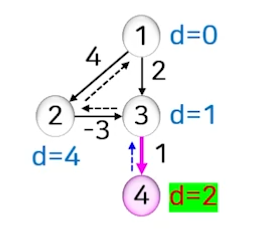
• 간선 3개를 사용한 최단 경로
  • 간선 <3,4>에 의해 d[4]가 3에서 2로 조정된다.

성능

• 바깥 for 루프는 정점의 개수만큼, 안쪽 for 루프는 간선의 개수만큼 반보가는 이중 for문 이므로 O((|V||E|))
• 음의 가중치를 갖는 간선이 없는 경우 데이크스트라 알고리즘이 더 효율적

모든 쌍 최단 경로

플로이드 알고리즘

• 동적 프로그래밍 방법
• 경로의 길이가 음인 사이클이 존재하지 않아야 한다.
• 경유할 수 있는 정점의 범위가 1인 경로부터 시작해서 |V|인 경로까지 하나씩 정점의 범위를 늘려가면서 모든 정점간의 최단 경로를 한꺼번에 구함
• 모든 정점 쌍 간의 최단경로는 행렬로 표현한다.

예제

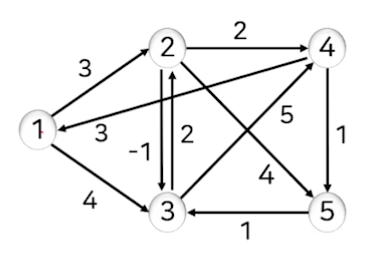
주어진 그래프에 대해서 플로이드 알고리즘을 적용하여 모든 정점 쌍 간의 최단 경로를 구하시오.

• D(0) : 인접 행렬의 값을 초기화한다. 행렬 표현에서 정점 i와 정점 j 사이에 간선이 없으면 ∞로 표현한다.

• D(1) : 경유할 수 있는 중간 정점 k=1을 이용하여 정점 i에서 정점 j까지 가는 최단 경로의 길이를 계산한다.
• 정점 4에서 정점 2까지의 최단 경로는 정점 1을 경유하여 가면 6이다.
• 정점 4에서 정점 3까지의 최단 경로는 정점 1을 경유하여 가면 7이다.

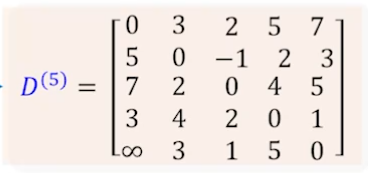
• 위의 과정을 적용하여 중간 정점으로 2,3,4,5를 각각 경로하는 최단 경로 D(2), D(3), D(4), D(5)를 구할 수 있다.

성능

• O(|V|³)
• 각 정점을 출발점으로 사용하여 데이크스트라 알고리즘을 반복적으로 적용해서도 해결 가능하지만 플로이드 알고리즘이 더 효율적
• |V|×|V| 크기의 배열 P[][]를 사용해서 최단 경로 자체를 구할 수 있음
  • 정점 k를 경유하는 경로의 길이가 경유하지 않는 경로의 길이보다 더 짧으면 P[i][j]에 중간 정점 k를 저장해서 활용

네트워크 플로

• 주어진 네트워크에 대해서 플로를 최대로 하는 값을 찾는 문제
• 네트워크 N=(V,E,s,t,c)
  • 방향 그래프 G=(V,E)
  • s : 소스 (시작점, 진입차수가 0인 정점)
  • t : 싱크 (도착점, 진출차수가 0인 정점)
  • c : 간선의 가중치, 간선의 용량
    • c(u,v) : 간선 <u,v>를 통해 보낼 수 있는 최대의 양/값
• 플로 f(u,v) → 간선 <u,v> 의 용량 중에서 실제 사용하고 있는 양/값
  • 용량 제약 조건 : 임의의 간선의 플로는 항상 0보다 크거나 같고, 해당 간선의 용량을 초과하지 못함
  • 플로 보존 제약 조건 : 소스/싱크를 제외한 모든 정점에 대해 어떤 정점으로 들어오는 양과 나가는 양은 동일
• 플로 값 F → 소스에서 나가는 플로의 합 또는 싱크로 들어오는 플로의 합

포드-풀커슨 알고리즘

• 네트워크 플로 문제에 최초로 제시된 가장 기초적인 해결 방법
• 모든 간선의 플로를 0으로 둔 상태에서 시작하여 증가 경로가 더 이상 존재하지 않을 때까지 반복적으로 경로를 찾아서 최대 플로 값을 구하는 방법
• 증가 경로 : 소스에서 싱크까지 더 많은 플로를 보낼 수 있는 경로
  • 순방향 간선 : 간선 <u,v>가 N의 간선의 방향과 같은 경우
  • 역방향 간선 : 간선 <u,v>가 N의 간선의 방향과 다른 경우
    • c(u,v)=0, f(u,v)=-f(v,u)
    • 남아 있는 모든 가능한 경로를 더 찾아낼 수 있게 하는 포드-풀커슨 방법의 핵심
• 잔여 용량 : 간선 <u,v>에서 추가로 플로를 증가시킬 수 있는 여유 용량
  • 순방향 간선 : 증가시킬 수 있는 양/값
  • 역방향 간선 : 원래 간선에 부여된 플로를 줄일 수 있는 양/값
• 증가 경로의 여유량 : 경로에 포함된 모든 간선의 잔여 용량 중 최소값

예제

주어진 네트워크에 대해서 포드-폴커슨 알고리즘을 적용하여 최대 플로를 구하시오.

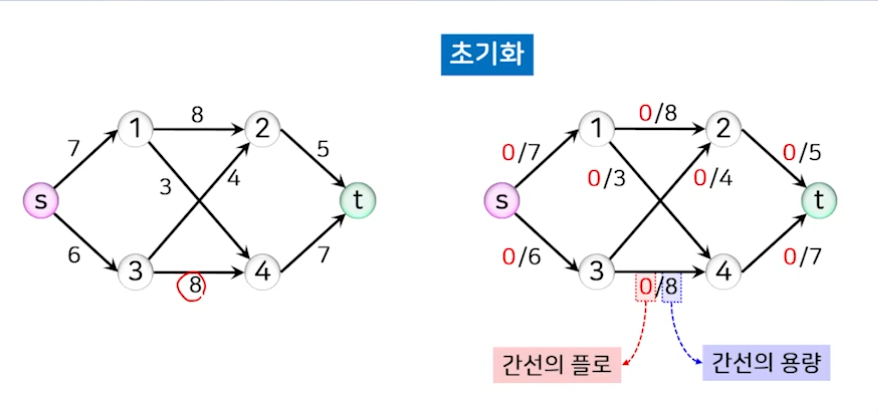
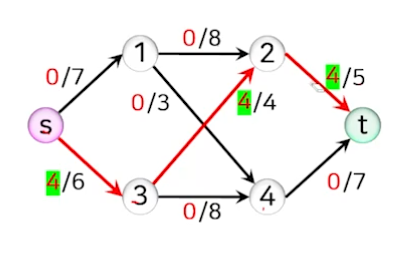
• 모든 간선의 플로를 0으로 초기화한다.
• 간선의 레이블은 ‘플로/용량’으로 나타낸다.

• 증가 경로를 반복해서 찾아야 하는데, 경로를 찾는 법칙이나 순서는 없다. 증가 경로 여유량은 0보다 커야 한다.
• 직관적인 증가 경로로서 s-1-2-t, s-3-4-t, s-1-4-t를 선택하면 역방향 간선 없이 간단히 최대 플로를 구할 수도 있다.
• 그러나 역방향 간선의 개념을 살피기 위해 s-2-3-t가 증가 경로로 선택되었다고 가정한다.
• 해당 경로의 여유량은 간선 <3,2>은 잔여 용량이 최소이므로 4가 되고, 경로상의 모든 간선은 순방향 간선이므로 플로를 4씩 증가시킨다.

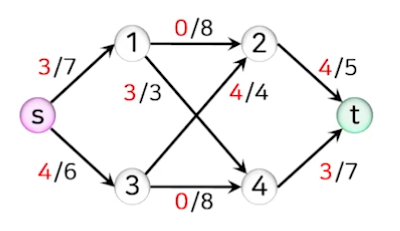
• 다시 증가 경로를 찾고 플로를 조정한다. 이번에는 증가 경로로서 s-1-4-t를 선택한다.
• 간선<1,4>의 잔여 용량이 3으로 최소이고, 모든 간선이 순방향 간선이므로 플로를 3씩 증가시킨다.

• 증가 경로 s-3-4-t를 선택하면 해당 경로의 여유량은 간선 <s,3>의 잔여 용량이 2로 최소이고, 모든 간선이 순방향 간선이므로 플로를 2씩 증가시킨다.

• 증가 경로 s-1-2-t를 선택하면 해당 경로의 여유량은 간선 <2,t>의 잔여 용량이 1로 최소이고, 모든 간선이 순방향 간선이므로 플로를 1씩 증가시킨다.

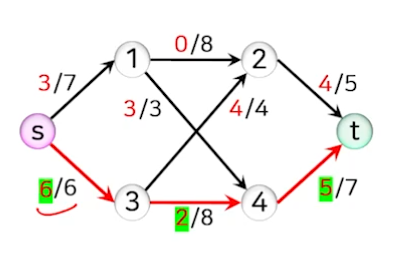
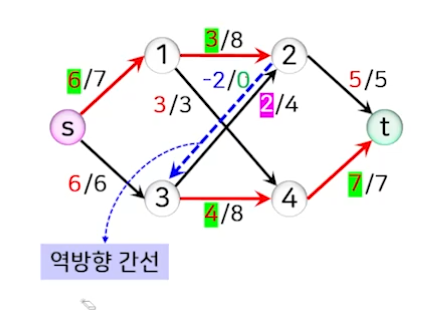
• 이번에는 증가 경로로 s-1-2-3-4-t를 선택하면 해당 경로의 여유량은 간선 <4,t>의 잔여 용량이 2로 최소이다.
• 순방향 간선에 대해서는 플로를 2만큼 증가시키고, 역방향 간선 <2,3>은 2만큼 감소시킨다.
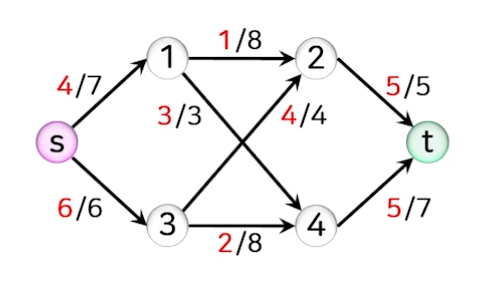
• 이제 더 이상 증가 경로가 존재하지 않으므로 최대 플로 F는 소스에서 나가는 플로의 합(6+6) 또는 싱크로 들어오는 플로의 합(5+7)인 12이다.

성능

• O(|E|F)
• 증가 경로를 선택할 때 깊이 우선 탐색 사용
  • 에드몬즈-카프 알고리즘에서는 너비 우선 탐색 적용
• 간선의 용량이 무리수이면 알고리즘이 종료하지 않을 수 있음
• 용량 M이 매우 큰 값이면 비효율적
• 커트 : 소스와 싱크가 각각 서로 다른 집합에 속하도록 정점 집합을 두 개의 집합으로 나누었을 때 두 집합을 연결하는 간선의 집합