[알고리즘] 그래프1

그래프

• 그래프 G = (V,E)
• 정점의 집합 V와 간선의 집합 E로 구성된 비선형 자료구조
• 방향성 여부에 따라 무방향 그래프와 방향 그래프로 구분된다.
• 간선에 비용이나 시간과 같은 의미를 갖는 가중치를 부여한 그래프를 가중 그래프라 한다.
• 정점 u에서 정점 v 사이의 간선을 무방향 그래프에서는 (u,v)로 표현하며, 방향 그래프에서는 <u,v>로 표현한다.

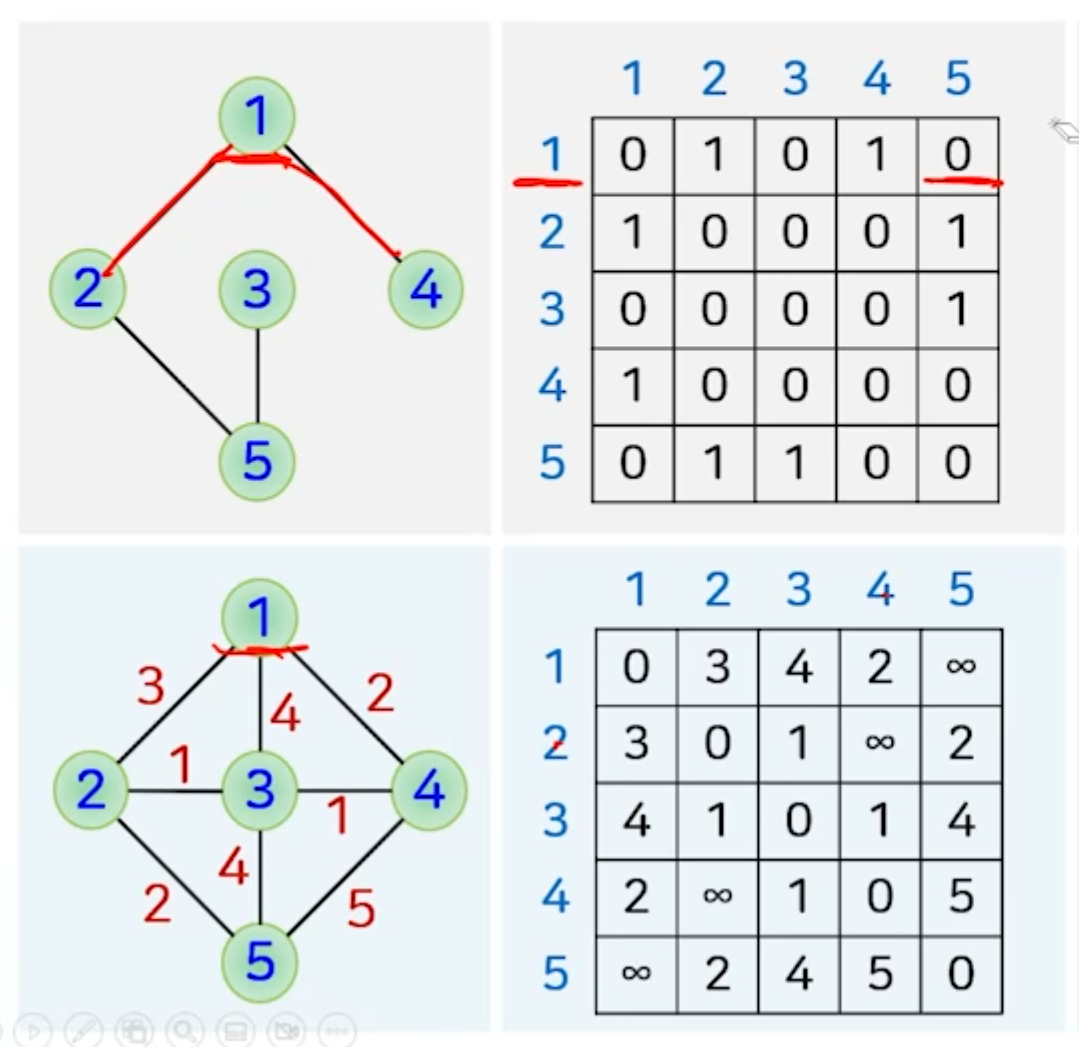
인접 행렬

• 그래프를 2차원 배열로 표현
• i=j인 대각선상의 값은 0이다.
• 일반 그래프 : 정점 i와 정점 j 사이에 간선이 존재하면 1, 존재하지 않으면 0이다.
• 가중 그래프 : 정점 i와 정점 j 사이에 간선이 존재하면 가중치 값, 존재하지 않으면 ∞이다.

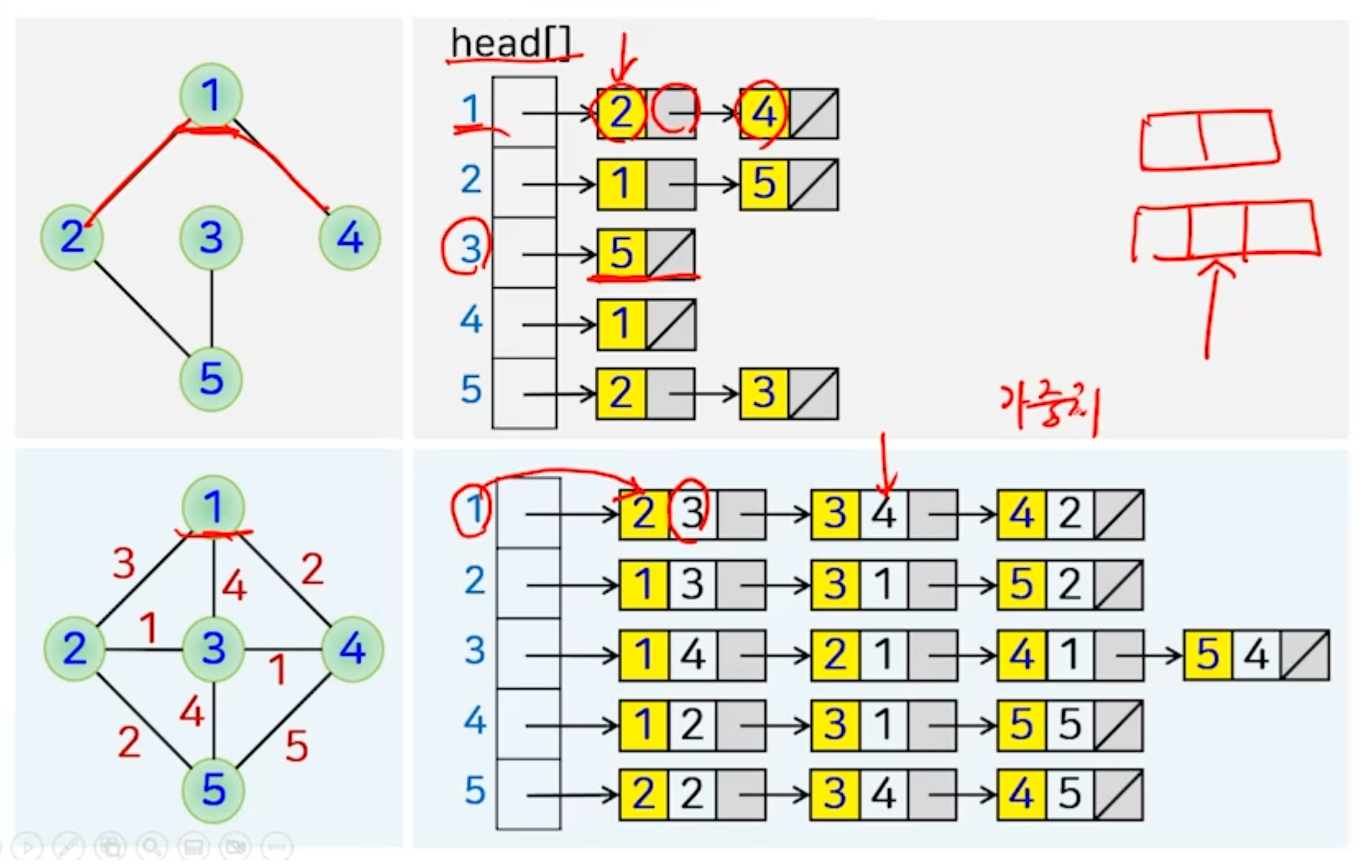
인접 리스트

• 그래프를 연결 리스트로 표현
• 임의의 정점 u를 중심으로 인접한 모든 정점을 하나의 연결 리스트로 표현
• 일반 그래프 : 정점을 나타내는 필드와 링크 필드로 구성
• 가중 그래프 : 가중치를 저장하기 위한 필드가 추가로 필요

let paths = [];

const BFS = (arr) => {
  let memo = {};
  for (let item of arr) {
    const [prev, next] = item;
    if (memo[prev]) {
      memo[prev].push(next);
    } else {
      memo[prev] = [next];
    }
  }
  console.log(memo);
  //   {
  //   '1': [ 2, 4 ],
  //   '2': [ 1, 5 ],
  //   '3': [ 5 ],
  //   '4': [ 1 ],
  //   '5': [ 2, 3 ]
  // }

  let visited = {};

  const DFS = (v, path) => {
    if (v === 5) {
      paths.push(path);
      return;
    }
    if (memo[v]) {
      visited[v] = true;
      for (let item of memo[v]) {
        //미방문 정점만 방문
        if (!visited[item]) {
          DFS(item, [...path, item]);
        }
      }
      visited[v] = false;
    }
  };

  DFS(1, [1]);
};

BFS([
  [1, 2],
  [1, 4],
  [2, 1],
  [2, 5],
  [3, 5],
  [4, 1],
  [5, 2],
  [5, 3]
]);
console.log(paths); //[[1,2,5]]

그래프 순회

• 방문 정점 : 방문이 완료된 정점
• 주변 정점 : 방문 정점에 인접한 정점 중에서 아직 방문하지 않은 정점

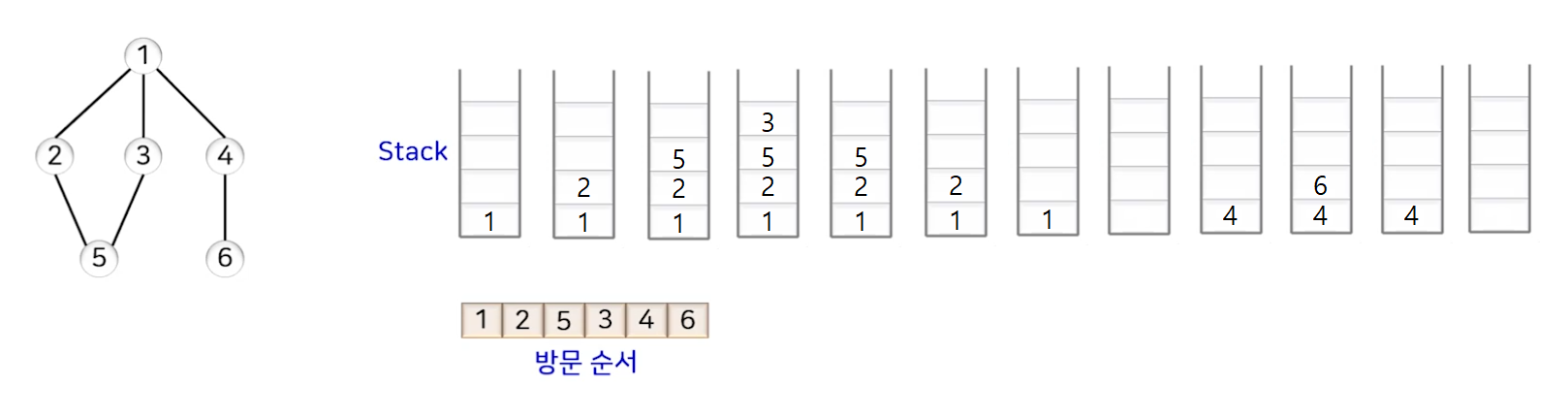
깊이 우선 탐색 (DFS)

• 스택 구조를 사용
• 최근의 주변 정점을 우선 방문
• 스택의 탑에 있는 정점에 대한 주변 정점이 존재하면 그중 하나의 정점을 스택에 삽입하고 방문한 정점으로 처리한다. 주변 정점이 없다면 스택의 탑에 있는 정점을 제거한다.

성능

• 인접 행렬로 표현하면 O(|V|²), 인접 리스트로 표현하면 O(|V|+|E|)
• 순환 알고리즘 형태로 쉽게 구현할 수 있다.

너비 우선 탐색 (BFS)

• 큐 구조를 사용
• 주변 정점 중에서 오래된 것을 우선 방문
• 시작 정점을 기준으로 가장 인접한 정점을 우선으로 모두 방문한 후 시작 정점과의 거리가 점점 멀어지는 순서로 인접 정점들을 탐색

성능

• 인접 행렬로 표현하면 O(|V|²), 인접 리스트로 표현하면 O(|V|+|E|)

위상 정렬

• 무사이클 방향 그래프에서 모든 간선이 한 방향으로만 향하도록 정점을 한 줄로 나열하는 것
• 깊이 우선 탐색을 활용하여 스택에서 삭제되는 정점을 역순으로 나열

성능

• 인접 행렬로 표현하면 O(|V|²), 인접 리스트로 표현하면 O(|V|+|E|)

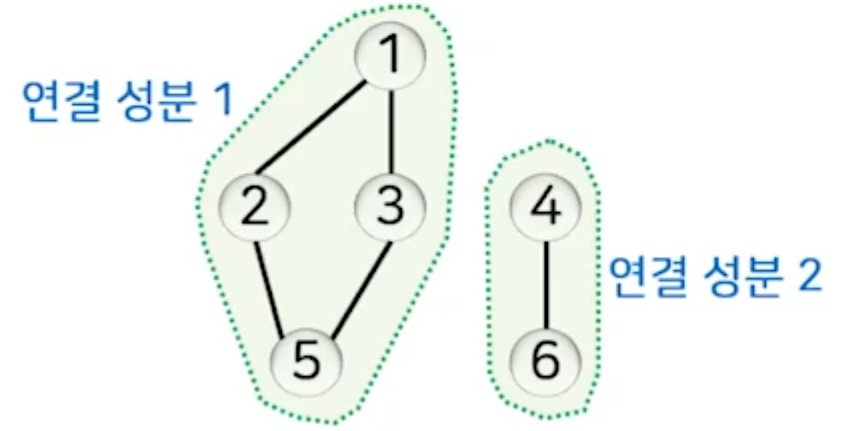
연결 성분

• 무방향 그래프에서 임의의 두 정점 간의 경로가 존재하는 최대 부분 그래프
• 깊이 우선 탐색이나 너비 우선 탐색을 활용하여 큐/스택이 비는 순간 그때까지 탐색한 정점들을 하나의 연결 성분으로 구성

강연결 성분

• 방향 그래프에서 임의의 두 정점 사이에 양방향의 경로가 존재하는 최대 부분 그래프
• (1) 깊이 우선 탐색으로 정점의 방문 완료 순서(방문 순서의 역순)를 구한다.
• (2) 모든 간선의 방향을 반대로 바꾼다.
• (3) 방문 완료 번호가 큰 것부터 깊이 우선 탐색을 수행하여 갈 수 있는 정점들의 각 리스트가 강연결 성분이 됨

최소 신장 트리

• 신장 트리
  • 가중 무방향 그래프에서 모든 정점을 포함하는 트리
  • 신장 트리에는 사이클이 존재하지 않는다.
  • 정점의 개수 |V|=n 이면 트리에는 정확히 n-1개의 간선이 존재한다.
• 간선들의 가중치들의 합이 가장 작은 신장 트리
• 최소 신장 트리를 구하는 방법에는 크루스칼 알고리즘, 프림 알고리즘이 있다. (둘 다 욕심쟁이 방법)

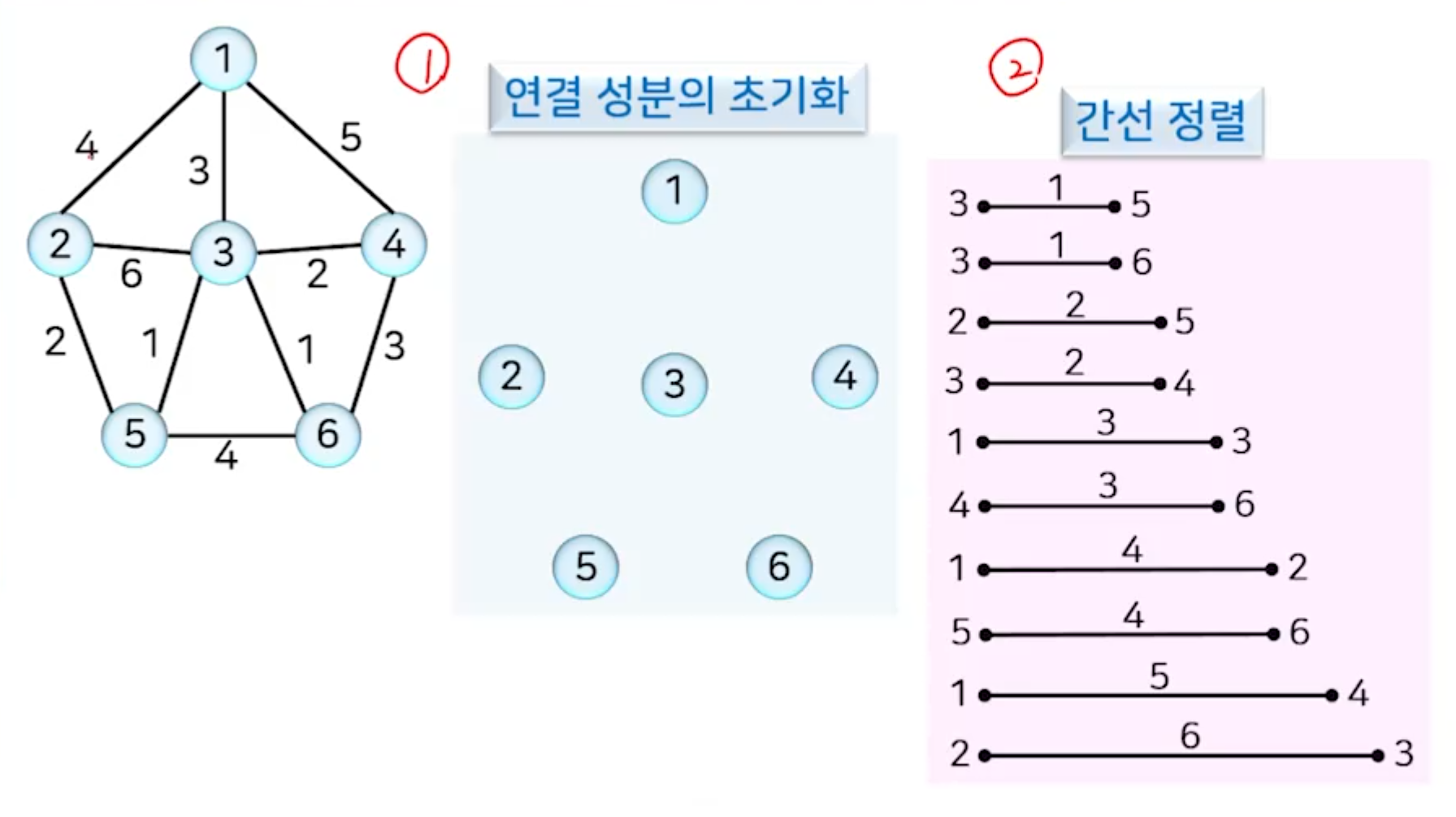
크루스칼 알고리즘

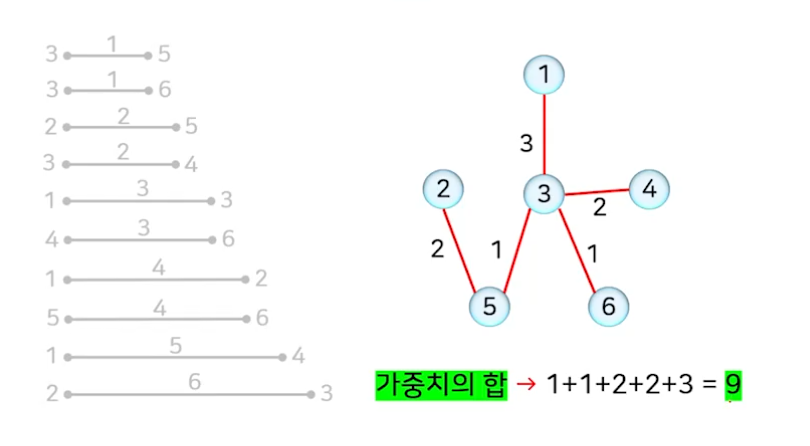
• 간선이 없는 상태에서 시작해서 가중치가 가장 작은 간선부터 하나씩 골라서 사이클을 형성하지 않으면 해당 간선을 추가하는 방식
• 간선 (u,v)의 두 정점 u,v가 서로 다른 연결 성분에 속하면 사이클을 형성하지 않음

간선 (4,6)부터는 사이클이 형성되어 선택할 수 없다.

성능

• O(|E|log|E|)

프림 알고리즘

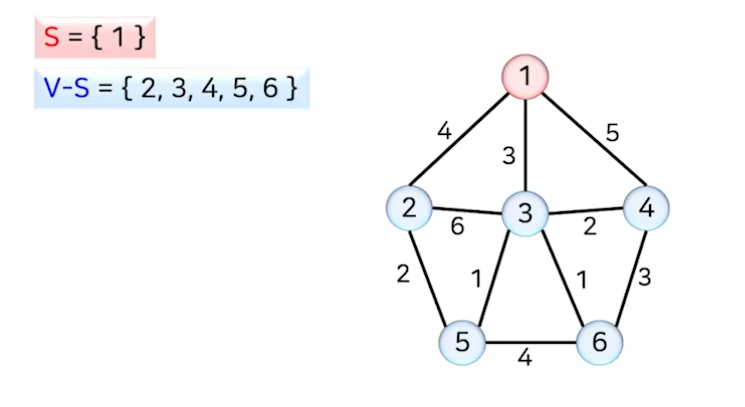
• 임의의 한 정점에서 시작해서 연결된 정점을 하나씩 선택해 나가는 방법
• 선택된 정점의 집합 S와 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선을 선택해서 추가하는 방법

• 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선 (1,3)을 선택해 T에 추가하고, 정점 3을 S에 추가한다.
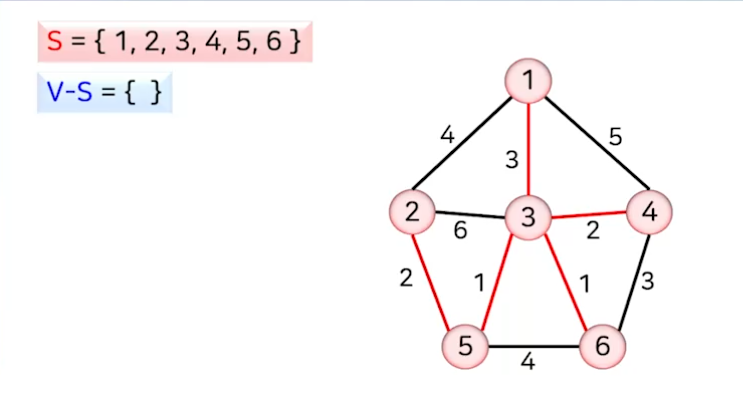
• 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선 (3,5)을 선택해 T에 추가하고, 정점 5을 S에 추가한다.
• 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선 (3,6)을 선택해 T에 추가하고, 정점 6을 S에 추가한다.
• 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선 (2,5)을 선택해 T에 추가하고, 정점 2을 S에 추가한다.
• 선택되지 않은 정점의 집합 V-S를 잇는 간선 중에서 가중치가 가장 작은 간선 (3,4)을 선택해 T에 추가하고, 정점 4을 S에 추가한다.

성능

• 인접 행렬로 표현하면 O(|V|²), 인접 리스트로 표현하면 O((|V|+|E|)log|V|)