[알고리즘] 정렬 알고리즘3 - 힙 정렬

힙 정렬

• 제자리 정렬 알고리즘이다.
• 힙 자료구조를 활용한 정렬 방법이다.
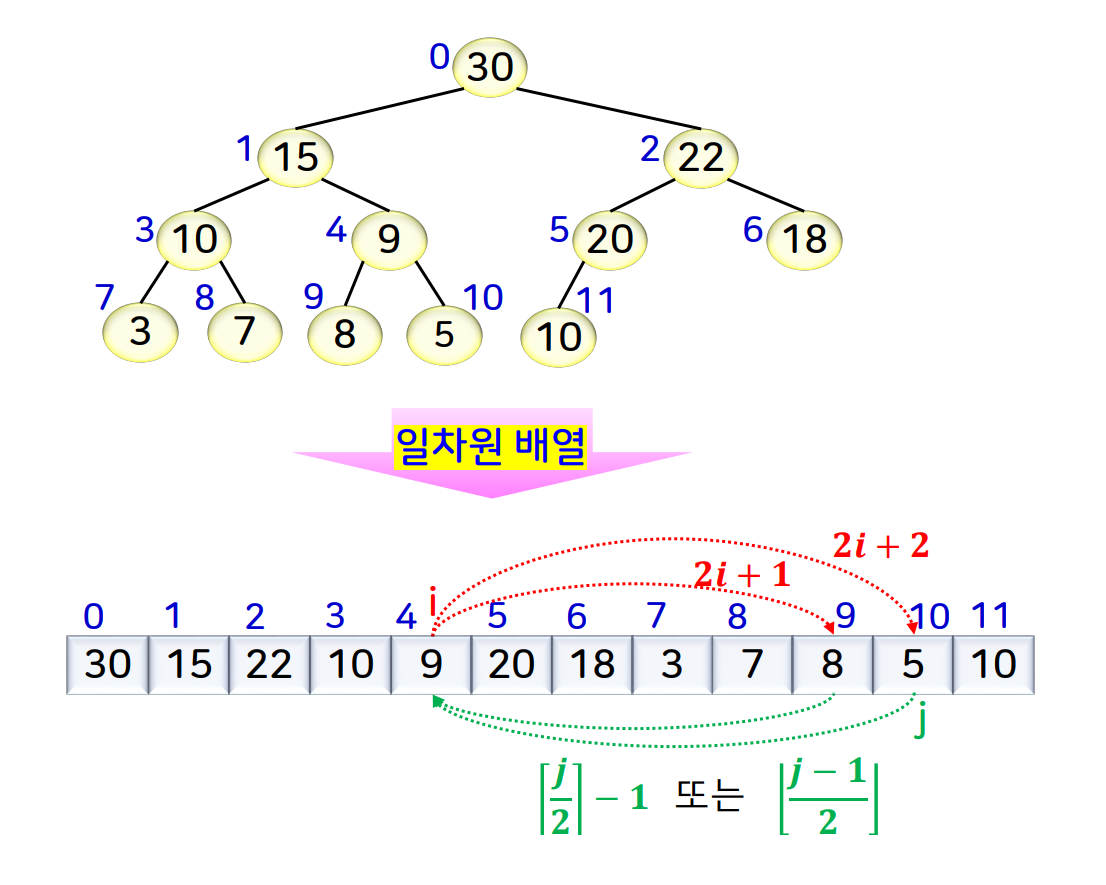
  • 완전 이진 트리
  • 각 노드의 값은 자신의 자식 노드의 값보다 크거나 같아야 함
• 임의의 값 삽입과 최댓값 삭제가 쉬움
• 간단한 인덱스 계산을 통해 부모/자식 노드에 접근할 수 있다.

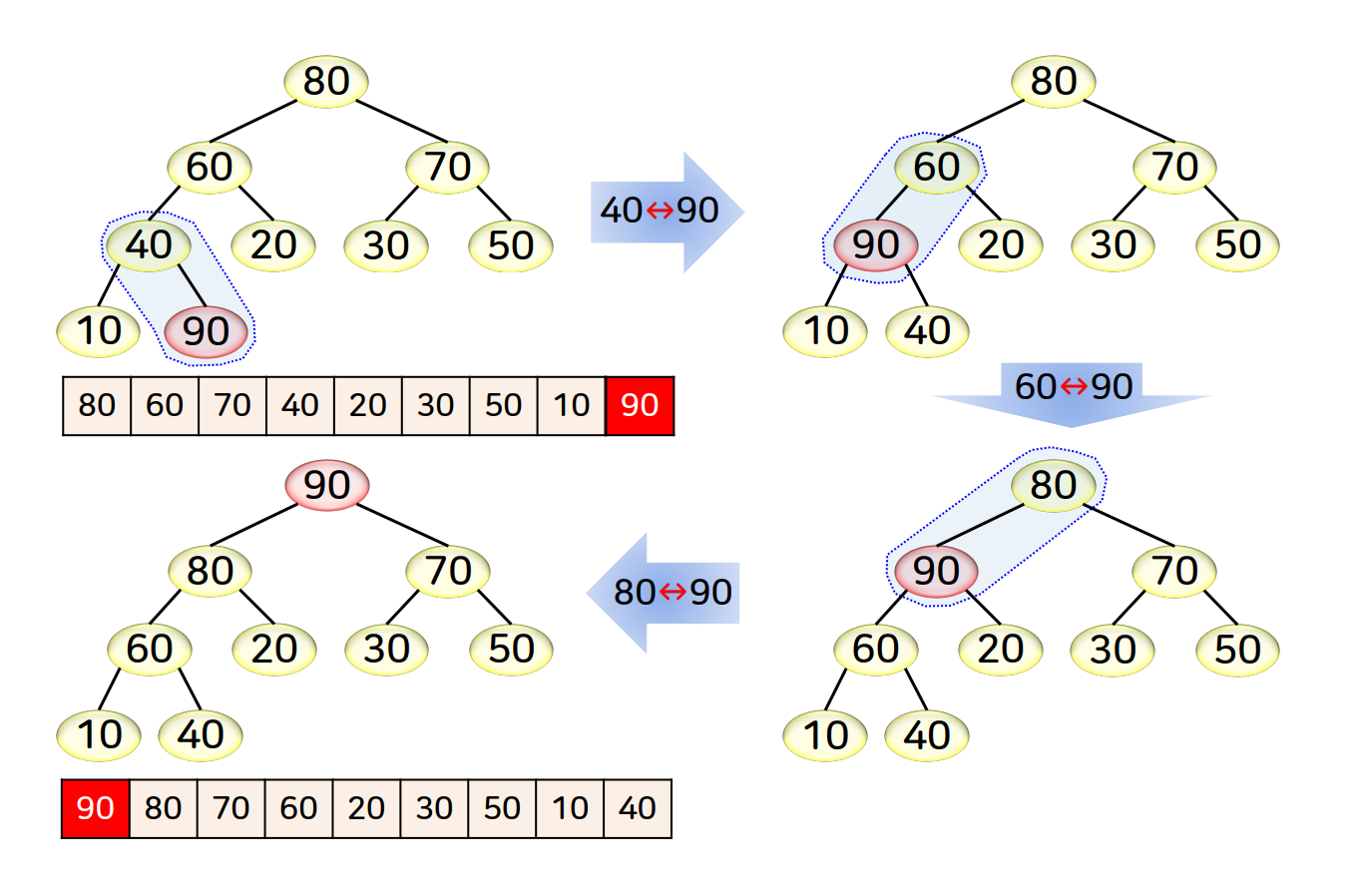
삽입

• 배열의 맨 뒤에 삽입한다.
• 부모 노드가 자식 노드보다 크거나 같아야 하는 조건을 만족할 때까지 위치를 이동한다.

삭제

• 배열의 첫 번째 원소(최댓값)와 마지막 원소의 위치를 교환한다.
• 배열의 마지막 원소(최댓값)를 삭제한다.
• 부모 노드가 자식 노드보다 크거나 같아야 하는 조건을 만족할 때까지 위치를 이동한다.

정렬

아래 단계를 통해 정렬한다.

• 단계 1 : 주어진 일차원 배열을 초기 힙으로 구축
• 단계 2 : 최댓값 삭제 및 힙으로 재구성하는 과정을 반복

단계 1의 주어진 일차원 배열을 초기 힙으로 구축하는 방법에는 두 가지가 있다.

• 배열의 원소를 순서대로 하나씩 트리에 추가하면서 힙의 조건을 만족하지 못하면 위치를 교환하는 방법이다.
• 배열을 우선 완전 이진 트리로 만든 후, 각 노드에 대해서 아래에서 위로, 오른쪽에서 왼쪽으로 진행하면서 해당 노드가 힙의 조건을 만족할 때까지 위치를 교환하는 방법이다.

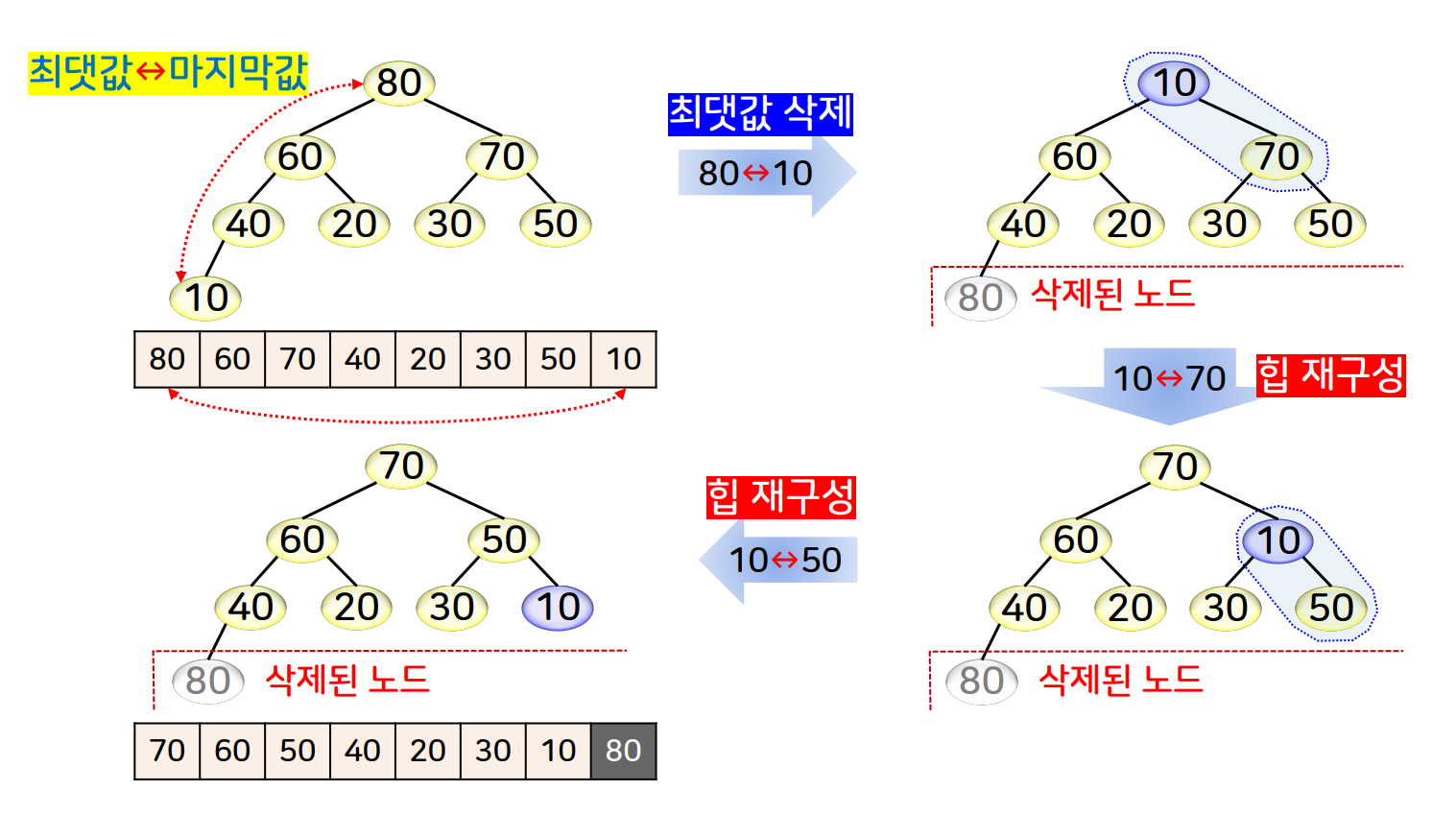
단계 2에서는 힙의 루트 노드의 값과 힙에서의 맨 마지막 노드의 값을 교환한 후, 루트 노드로부터 리프 노드로 진행하면서 힙의 조건을 만족하도록 조정하는 과정을 반복한다.

• 루트 노드(최댓값)와 마지막 노드의 위치를 서로 교환한다.
• 루트 노드가 힙의 조건을 만족할 때까지 자식 노드와 위치를 교환한다.
• 다시 루트 노드와 마지막 노드의 위치를 서로 교환하여 반복한다.

시간복잡도

• 최선: O(nlogn)
• 평균: O(nlogn)
• 최악: O(nlogn)