[알고리즘] 정렬 알고리즘2 - 분할 정복

분할 정복 알고리즘

• 주어진 문제를 독립적인 소문제로 분할하여 해결하는 방법이다.
• 순환할 때마다 분할, 정복, 결합 세 단계를 거친다.

퀵 정렬

• 분할 정복 방법이 적용된 알고리즘이다. (결합 단계는 필요하지 않다.)
• 제자리 정렬 알고리즘이다.
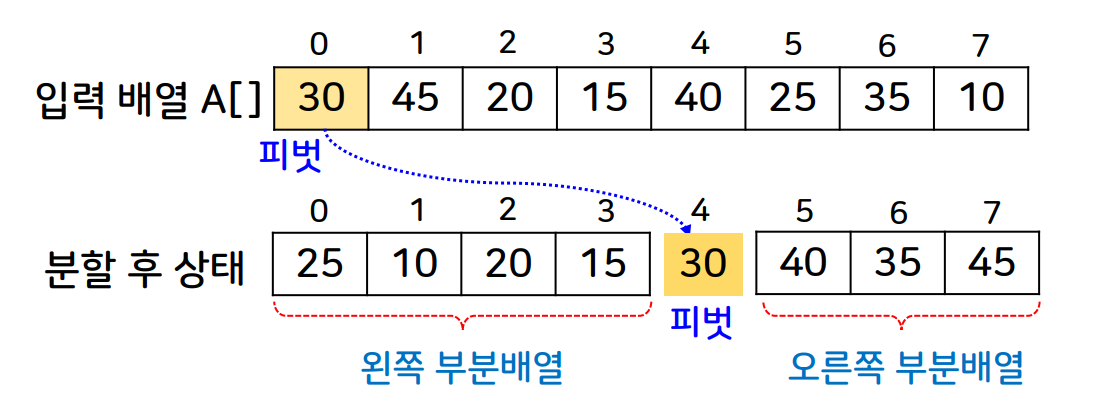
• 피벗(pivot)을 기준으로 배열을 피벗보다 작은 배열과 피벗보다 큰 배열로 분할하고 이렇게 분할한 배열에 다시 퀵 정렬을 순환적으로 적용한다.
• 배열이 이미 정렬된 경우 배열이 2개로 분할되지 않으므로 최악의 시간 복잡도를 가진다.

예시

function swap(arr, i, j) {
  const temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

function partition(arr, start, end) {
  let pivot = arr[start];
  let left = start + 1;
  let right = end;

  while (left < right) {
    for (let i = left; i < end; i++) {
      if (arr[left] >= pivot) break;
      else left++;
    }
    for (let i = right; i > start; i--) {
      if (arr[right] < pivot) break;
      else right--;
    }

    //left가 right과 같거나 클 때 left++,right--를 하지 않아야 right과 피벗을 교환했을 때 정상적으로 정렬된다.
    if (left < right) {
      swap(arr, left, right);
      left++;
      right--;
    }
  }

  if (arr[start] > arr[right]) {
    swap(arr, start, right);
  }

  return right;
}

function quickSort(arr, start = 0, end = arr.length - 1) {
  if (start < end) {
    const pivot = partition(arr, start, end);
    quickSort(arr, start, pivot - 1);
    quickSort(arr, pivot + 1, end);
  }
  return arr;
}

const arr = [30, 45, 20, 15, 40, 25, 35, 10];
quickSort(arr);

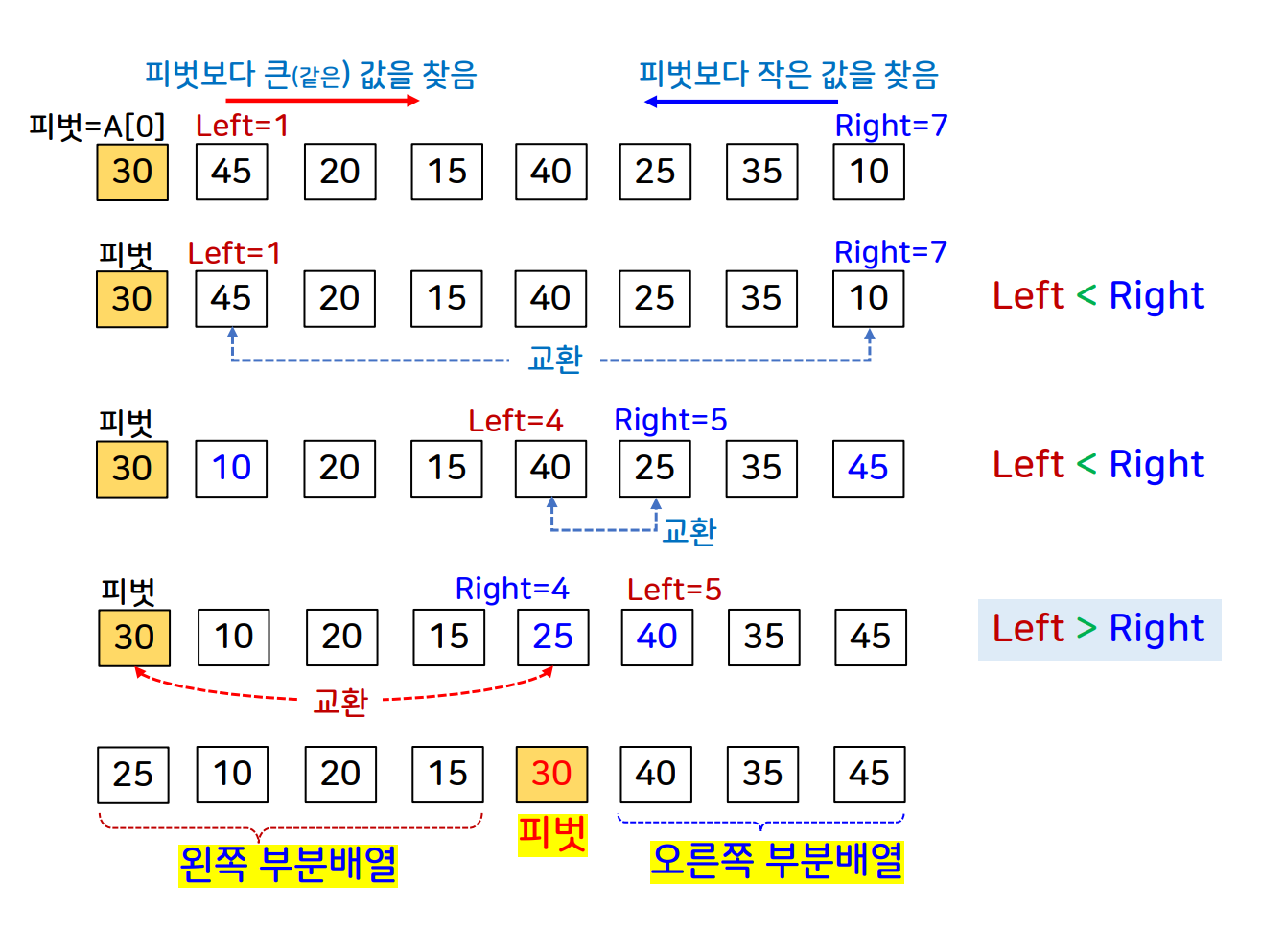
• 처음 피벗은 배열의 0번째 인덱스로 하며 분할함수에서 피벗의 인덱스를 리턴한다.
• 분할함수에서는 배열의 왼쪽과 오른쪽에서부터 피벗과 비교하면서 피벗보다 작은 요소를 발견하면 피벗의 index와 swap한다.

시간 복잡도

• 최선: O(nlogn) (피벗 선택의 임의성이 보장된 경우)
• 평균: O(nlogn)
• 최악: O(n^2) (배열이 이미 정렬된 경우)

합병 정렬

• 분할 정복 방법이 적용된 알고리즘이다.
• 안정적인 정렬 알고리즘이다.
• 제자리 정렬 알고리즘이 아니다.
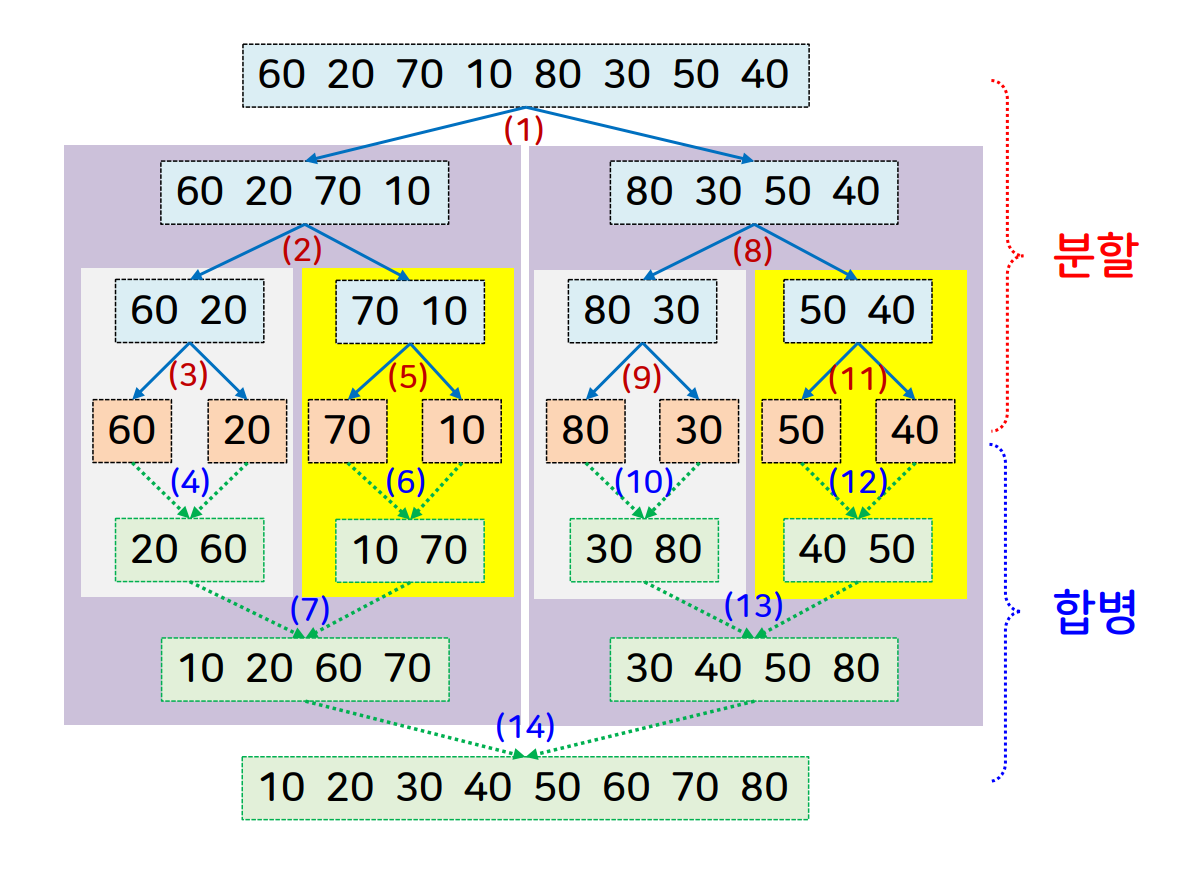
• 입력 배열을 동일한 크기의 두 부분배열로 분할하고, 각 부분배열을 순환적으로 합병 정렬한 뒤 합병하여 하나의 정렬된 배열을 만든다.

예시

function merge(leftArr, rightArr) {
  console.log("merge", leftArr, rightArr);

  let result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < leftArr.length && rightIndex < rightArr.length) {
    //부분배열 leftArr[leftIndex]와 rightArr[rightIndex]를 비교하여 작은 순서대로 result에 push
    if (leftArr[leftIndex] < rightArr[rightIndex]) {
      result.push(leftArr[leftIndex]);
      leftIndex++;
    } else {
      result.push(rightArr[rightIndex]);
      rightIndex++;
    }
  }

  // 남아 있는 데이터 result로 이동
  while (leftIndex < leftArr.length) {
    result.push(leftArr[leftIndex]);
    leftIndex++;
  }
  while (rightIndex < rightArr.length) {
    result.push(rightArr[rightIndex]);
    rightIndex++;
  }

  return result;
}

function mergeSort(arr) {
  console.log("merge", leftArr, rightArr);

  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const leftArr = arr.slice(0, mid);
  const rightArr = arr.slice(mid);
  return merge(mergeSort(leftArr), mergeSort(rightArr));
}

const arr = [60, 10, 20, 50];
mergeSort(arr);

• 입력 배열의 길이가 1이 될 때까지 mergeSort가 순환 호출된다.
• 입력 배열이 모두 길이가 1인 배열로 쪼개지면 merge가 순환 호출된다.
• 두 부분배열을 비교하며 정렬한 후 합병을 반복한다.
• 콘솔을 찍어봤을 때 아래와 같다.
  • ‘mergeSort’ [ 60, 10, 20, 50 ] ‘mergeSort’ [ 60, 10 ] ‘mergeSort’ [ 60 ] ‘mergeSort’ [ 10 ] ‘mergeSort’ [ 20, 50 ] ‘mergeSort’ [ 20 ] ‘mergeSort’ [ 50 ] ‘merge’ [ 60 ] [ 10 ] ‘merge’ [ 20 ] [ 50 ] ‘merge’ [ 10, 60 ] [ 20, 50 ]

시간 복잡도

• 최선: O(nlogn)
• 평균: O(nlogn)
• 최악: O(nlogn)

정리

구분	안정적인 정렬 알고리즘	제자리 정렬 알고리즘	시간복잡도(최선)	시간복잡도(평균)	시간복잡도(최악)
퀵 정렬	X	O	O(nlogn)	O(nlogn)	O(n^2)
합병 정렬	O	X	O(nlogn)	O(nlogn)	O(nlogn)

참고사이트

JavaScript로 Quick Sort(퀵 정렬) 구현하기