[알고리즘] 정렬 알고리즘1

정렬 알고리즘

• 입력 배열의 데이터를 크기 순서대로 재배치하는 것을 정렬(sort)이라고 한다.
• 동일한 값을 가진 데이터의 상대적 위치가 정렬 후에도 유지되면 안정적 정렬 알고리즘이다.
• 입력 배열 이외에 별도로 필요한 저장 공간이 상수 개를 넘지 않는 정렬 알고리즘을 제자리 정렬 알고리즘이라고 한다.

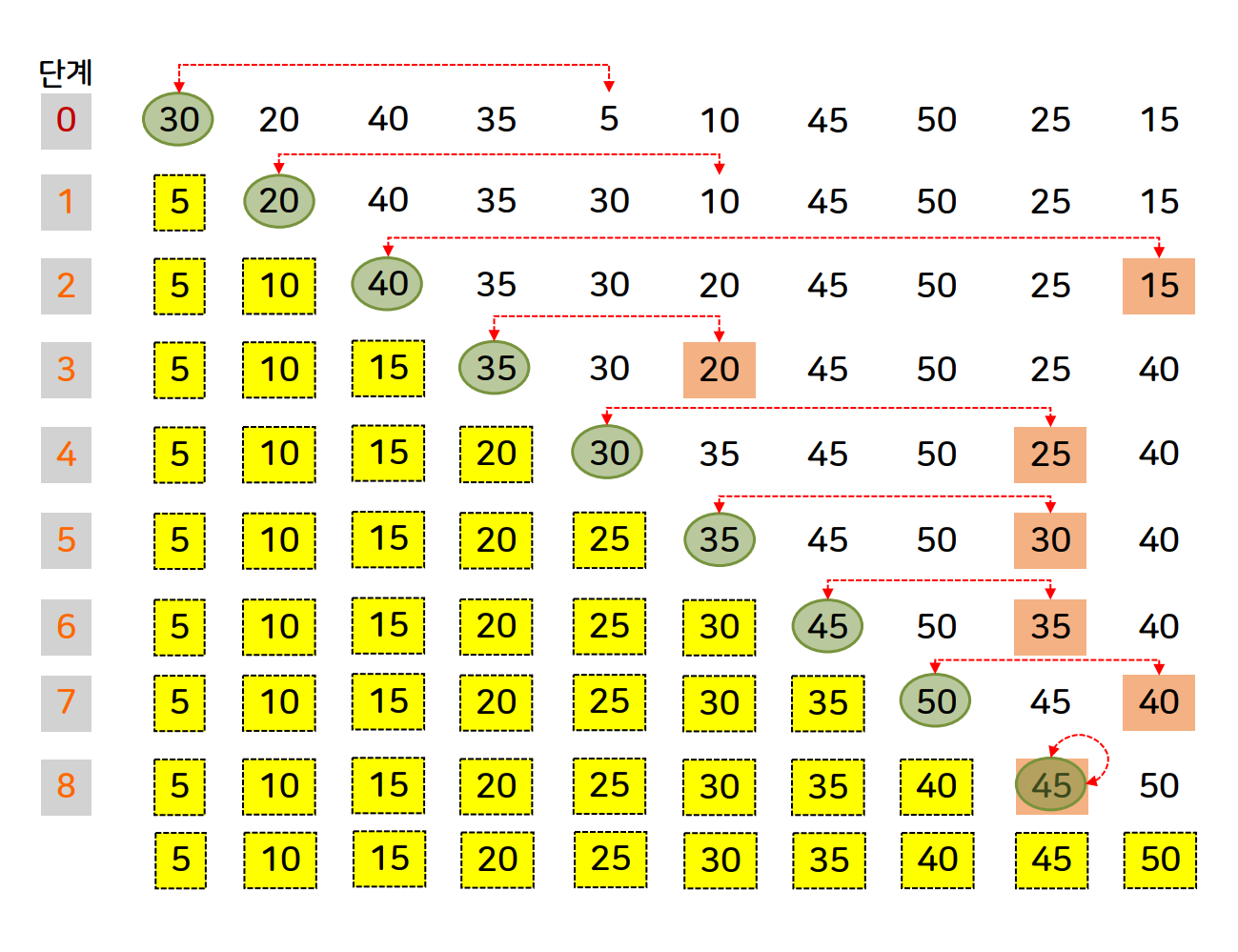
선택 정렬

• 제자리 정렬 알고리즘이다.
• 미정렬 부분에서 최솟값을 찾아서 미정렬 부분의 첫 번째 데이터와 위치를 교환하며 정렬하는 방식이다.

예시

function selectionSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex !== i) {
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    }
  }
  return arr;
}

• 배열을 2중 for문으로 순회하며 arr[minIndex]보다 작은 최소값 index을 찾는다. minIndex의 초기값은 i이다.
• 최소값을 찾은 후 현재 요소와 배열 순서를 교환한다. (ex. [arr[j], arr[minIndex]] = [arr[minIndex], arr[j]])
• 이 과정을 통해 가장 작은 값이 첫 번째 인덱스로 이동하고, 그 다음 작은 값이 첫 번째 인덱스 뒤부터 차례로 정렬된다.
• i 값이 커질때마다 첫 번째 인덱스부터 정렬되므로 안쪽 for문은 let j = i + 1; j < arr.length; 조건으로 순회한다.

시간 복잡도

• 최선: O(n^2)
• 평균: O(n^2)
• 최악: O(n^2)

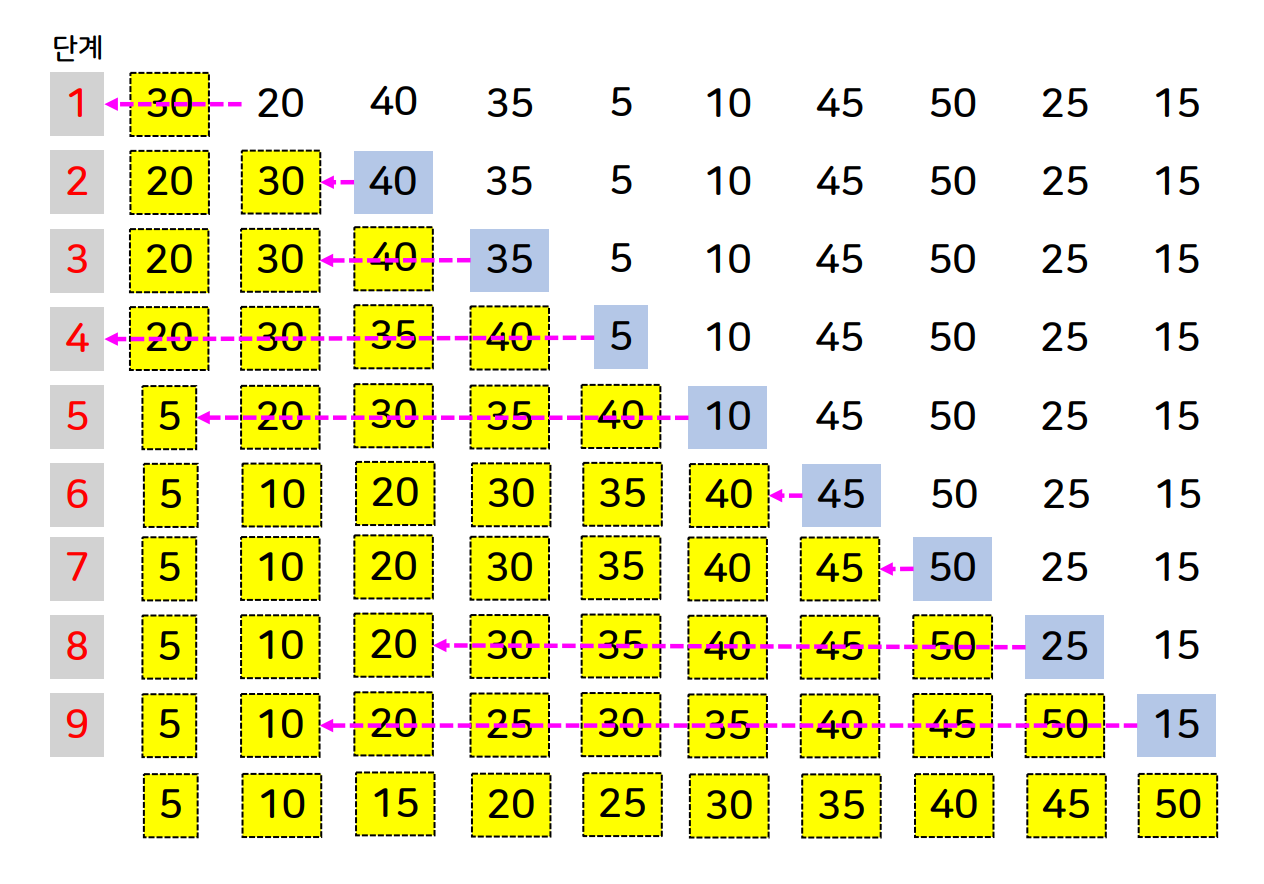
버블 정렬

• 안정적인 정렬 알고리즘이다.
• 제자리 정렬 알고리즘이다.
• 인접한 두 데이터를 비교해가면서 왼쪽 데이터가 오른쪽 데이터보다 큰 경우 위치를 교환하는 방식이다.

예시

function bubbleSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    let sorted = true; //이미 정렬된 상태라고 가정

    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        sorted = false; //swap 발생 = 미정렬 상태
      }
      if (sorted) break; // 이미 정렬된 상태이므로 종료
    }
  }
  return arr;
}

• 배열을 2중 for문으로 순회하며 인접한 두 요소를 비교한다.
• 뒤에 있는 요소가 더 작으면 위치를 교환한다. ([arr[j], arr[j + 1]] = [arr[j + 1], arr[j]])
• 이 과정을 통해 가장 큰 값이 마지막 인덱스로 이동하고, 그 다음 큰 값이 마지막 인덱스 앞부터 차례로 정렬된다.
• i 값이 커질때마다 마지막 인덱스부터 정렬되므로 안쪽 for문은 let j = 0; j < arr.length - i - 1 조건으로 순회한다.

시간 복잡도

• 최선: O(n) (배열이 이미 정렬된 경우)
• 평균: O(n^2)
• 최악: O(n^2)

삽입 정렬

• 안정적인 정렬 알고리즘이다.
• 제자리 정렬 알고리즘이다.
• 미정렬 부분에서 첫 번째 데이터를 뽑은 후 정렬 부분에서 데이터가 위치할 자리를 찾아서 삽입하는 방식이다.

예시

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let tmp = arr[i];
    let j;
    for (j = i - 1; j >= 0 && arr[j] > tmp; j--) {
      arr[j + 1] = arr[j];
    }
    arr[j + 1] = tmp;
  }
  return arr;
}

• 배열을 2중 for문으로 순회하며 i는 1 인덱스부터 시작하여 점점 커지고, j는 i-1부터 시작하여 점점 작아진다.
• 변수 j의 스코프는 for문 바깥에 있다. 그래서 for문이 break 되지 않고 전부 순환되어 끝나면 j의 값은 -1이 된다.
• arr[j]와 tmp 값을 비교하여 arr[j] 값이 더 크면 j+1 인덱스에 arr[j]를 삽입한다.
• arr[j]와 tmp 값을 비교하여 arr[j] 값이 더 크지 않으면 break한다.
• for문이 끝나면 마지막 j+1 인덱스에 tmp를 삽입한다.
• 안쪽 for문에 arr[j] > tmp 조건을 붙이면 배열이 이미 정렬된 경우 시간복잡도를 최적화 할 수 있다.

시간 복잡도

• 최선: O(n) (배열이 이미 정렬된 경우)
• 평균: O(n^2)
• 최악: O(n^2)

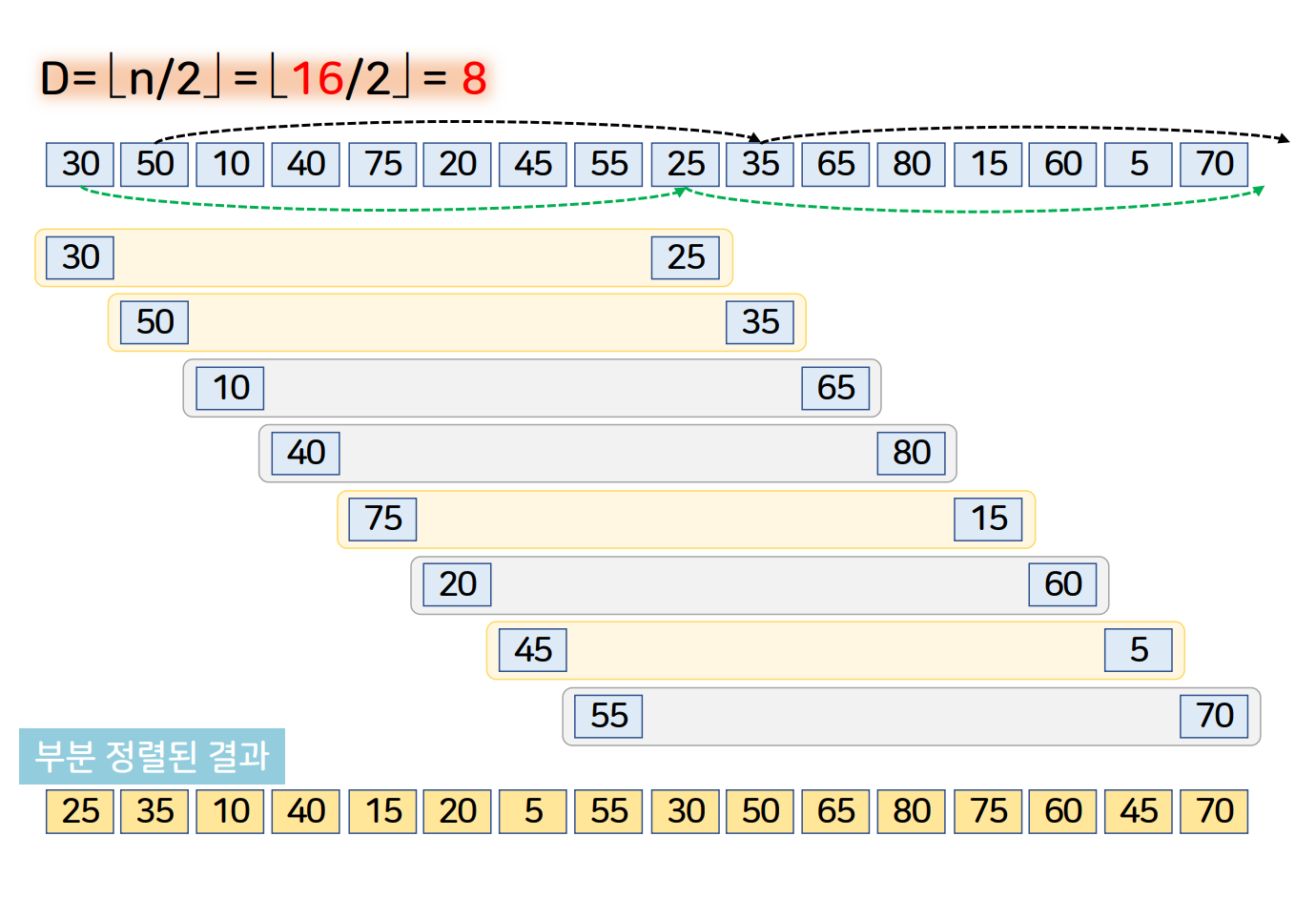
셸 정렬

• 제자리 정렬 알고리즘이다.
• 삽입 정렬의 단점을 보완할 수 있는 알고리즘이다. (하지만 최선의 시간복잡도는 삽입 정렬이 더 좋다.)
• 삽입정렬은 데이터를 하나씩 비교하지만 셸 정렬은 멀리 떨어진 데이터와 비교하여 처리 속도 향상
• 간격에 따라 성능이 달라진다. 가장 좋은 간격을 찾는 것은 아직 미해결 과제이다.

예시

function shellSort(arr) {
  const n = arr.length;
  //gap: 부분배열의 개수 & 간격의 크기
  for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
    //gap개의 부분배열에 대한 삽입 정렬
    for (let i = gap; i < n; i += 1) {
      const temp = arr[i];
      let j;
      for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
        arr[j] = arr[j - gap];
      }
      arr[j] = temp;
    }
  }
  return arr;
}

• 입력 배열을 n/2로 나눈 gap 간격만큼 떨어진 데이터들을 비교하여 삽입 정렬한다.
• gap이 1이 될 때까지 반복 수행한다.

시간 복잡도

• 최선: O(nlogn) (배열이 이미 정렬된 경우)
• 평균: O(n^2)
• 최악: O(n^2)

정리

구분	안정적인 정렬 알고리즘	제자리 정렬 알고리즘	시간복잡도(최선)	시간복잡도(평균)	시간복잡도(최악)
선택 정렬	X	O	O(n^2)	O(n^2)	O(n^2)
버블 정렬	O	O	O(n)	O(n^2)	O(n^2)
삽입 정렬	O	O	O(n)	O(n^2)	O(n^2)
셸 정렬	X	O	O(nlogn)	O(n^2)	O(n^2)

참고사이트

삽입 정렬