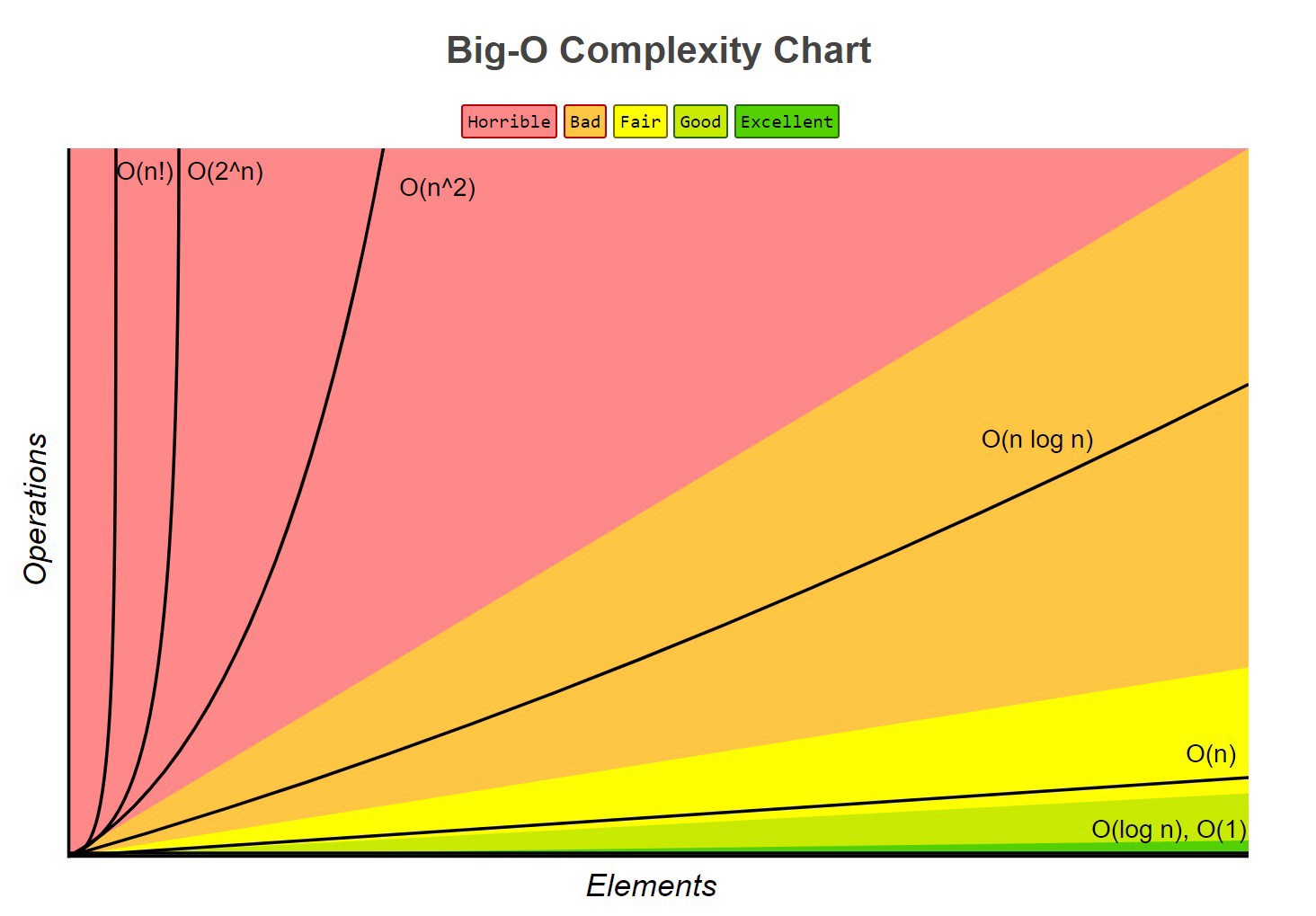
알고리즘 시간복잡도, Big-O
시간복잡도와 Big-O
시간 복잡도는 알고리즘을 처리하는 데 걸리는 시간을 정량화한 것이다.
Big-O를 통해 시간 복잡도를 표현할 수 있다.
O(1) : Constant Time
입력 데이터의 크기와 상관없이 언제나 일정한 시간이 걸린다.
ex) pop(), push() 등
1
2
3
const names = ["Luis", "John", "Jose"];
names.push("Aaron");
console.log(names); // (4) ["Luis", "John", "Jose", "Aaron"]
O(n) : Linear Time
입력 데이터의 크기와 처리 시간이 비례한다.
ex) for문, map(), filter() 등
1
2
3
4
const fruits = ["apple", "banana", "cherry", "orange"];
for (let i = 0; i < fruits.length; i++) {
console.log(fruits[i]);
}
O(n^2) : Quadratic Time
입력 데이터 크기의 제곱만큼 처리시간이 걸린다.
데이터의 길이가 늘어날 때마다 처리시간이 크게 증가한다.
ex) 2중 for문 등
1
2
3
4
5
6
const fruits = ["apple", "banana", "cherry", "orange"];
for (let i = 0; i < fruits.length; i++) {
for (let j = 0; j < fruits.length; j++) {
console.log(fruits[i] === fruits[j]);
}
}
O(2^n)
ex) 피보나치 수열 : 입력한 숫자 번째의 피보나치 수열에서 전 값과 전전 값을 더한다. (5->3+2, 6->5+3)
전 숫자와 전전 숫자를 재귀 함수로 전달하므로 함수가 호출될 때마다 두 번씩 호출된다.
O(n^2)보다 데이터의 증가에 따른 처리시간이 더 크다.
1
2
3
4
5
6
7
8
const fibonacci = (num) => {
// if(num < 0) return 0;
if (num < 2) {
return num;
} else {
return fibonacci(num - 1) + fibonacci(num - 2);
}
};
O(log n)
ex) 이진 탐색(Binary Search)
배열을 반으로 나눠가며 값의 위치를 탐색한다.
데이터의 양이 많아도 절반씩 줄이며 탐색하기 때문에 시간복잡도가 낮다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function binarySearch(sortedArray, key) {
let start = 0;
let end = sortedArray.length - 1;
while (start <= end) {
let middle = Math.floor((start + end) / 2);
// Math.ceil을 써도 같은 결과 출력
if (sortedArray[middle] === key) {
// found the key
return middle;
} else if (sortedArray[middle] < key) {
// continue searching to the right
start = middle + 1;
} else {
// search searching to the left
end = middle - 1;
}
}
// key wasn't found
return -1;
}
Big-O 계산 규칙
Worst Case
1
2
3
4
5
6
const fruits = ["apple", "banana", "cherry", "orange"];
for (let i = 0; i < fruits.length; i++) {
if (fruits[i] === "banana") {
return console.log(fruits[i]);
}
}
위 코드의 for문에서 중간에 원하는 요소를 찾으면 return 되어 중단된다.
하지만 Worst Case, 즉 최악의 경우를 고려하면 찾는 요소가 배열의 맨 마지막에 있을 수 있으므로 중간에 return을 하더라도 Big-O는 변하지 않는다.
Remove Constants
1
2
3
4
5
6
7
8
9
10
11
12
13
14
function printItems(items) {
console.log(items[0]); // O(1)
let middleIndex = Math.floor(items.length / 2);
let index = 0;
while (index < middleIndex) {
// O(n/2)
console.log(items[index]);
index++;
}
for (let i = 0; i < 100; i++) {
// O(100)
console.log("hi");
}
}
위 코드의 Big-O를 계산하면 O(1 + n/2 + 100)이다.
그러나 만약 items의 크기가 엄청나게 커진다면, 1을 더하든 100을 더하든 상관 없어진다.
결국 이 경우에도 Big-O는 O(1 + n/2 + 100)에서 상수를 제거한 O(n)이다.
1
2
3
4
5
6
7
8
9
10
function compareBoxes(boxes) {
boxes.forEach(function (boxes) {
// O(n)
console.log(boxes);
});
boxes.forEach(function (boxes) {
// O(n)
console.log(boxes);
});
}
위 코드도 O(2n)이지만 마찬가지로 상수를 제거하면 O(n)이다.
Big-O 계산은 정확한 속도를 계산하려고 하는 것이 아니라는 것을 기억하자.
Different Terms for Inputs
1
2
3
4
5
6
7
8
9
10
function compareBoxes(boxes, boxes2) {
boxes.forEach(function (boxes) {
// O(a)
console.log(boxes);
});
boxes2.forEach(function (boxes2) {
// O(b)
console.log(boxes);
});
}
위 코드의 경우는 함수의 인자 값이 다르므로 따로 계산을 해야 한다.
이 경우 Big-O는 O(a+b)이다.
Drop Non Dominants
1
2
3
4
5
6
7
8
9
10
11
12
function printAllNumber(numbers) {
numbers.forEach(function (number) {
// O(n)
console.log(number);
});
numbers.forEach(function (firstNumber) {
numbers.forEach(function (secondNumber) {
console.log(firstNumber + secondNumber); // O(n^2)
});
});
}
printAllNumber([1, 2, 3, 4, 5]);
위 코드는 O(n + n^2)이지만 배열의 길이가 커질수록 n^2가 압도적으로 커지기 때문에 결국 Big-O는 O(n^2)이다.
참고사이트
[자료구조] 시간복잡도 with JavaScript
자바스크립트 Array 메소드 및 예제에 대한 시간 복잡도 Big O